Anomalie #328
ouvertFrottement (LOI_COULOMB) : difficulté à mettre en place un calcul test
Description
Bonjour Gérard,
comme tu le sais, j'ai commencé à regarder le frottement. J'ai commencé par un cas test d'un élément hexaèdre en glissement contre un autre élément hexaèdre.
Le calcul est en 2 étapes :
1) mise en contact des 2 cubes (une force ponctuelle de -0.25 sur 4 noeuds donc total de 1 N selon -Z vient appuyer le petit cube contre le grand cube)
2) translation du petit cube dans la direction Y par déplacement imposé
Je définis une loi LOI_COULOMB pour avoir un coef de frottement (statique) de 0.1. Je m'attend donc à 2 choses :
1) dans le premier step => récupérer une force de réaction de 1 N selon Z sur le grand cube (colonne 11 du .maple)
2) dans le second step => toujours 1 N selon Z sur le grand cube + il faut obtenir une force de réaction sur le petit cube de -0.1 N selon Y (colonne 3 du .maple)
Voici les 3 problèmes que j'ai observés :
1) déjà premier constat : si j'active la loi de frottement, j'obtiens segmentation fault dès le premier incrément
======================================================================
INCREMENT DE CHARGE : 1 intensite 0.05 t= 0.05 dt= 0.05
======================================================================
==> LesContacts::Def Elem Cont, initialement 4 elem contact
apres Def Elem Cont: 4 elem contact Segmentation fault
j'ai essayé les 3 options de régularisation (loi_frottement_2) en mettant epsil= 1. et en testant regularisation= 1, 2 ou 3. Pas de changement, même message d'erreur.
2) j'ai testé juste la partie contact en supprimant le frottement pour voir si cette partie fonctionne comme prévu. Le calcul tourne correctement. J'obtiens une force de contact (FORCE_CONTACT) de 0.25 sur chaque noeud en contact, donc un total de 1N
=> par contre, je n'ai rien en force de réaction sur le grand cube (colonne 11 devrait etre égale à 1 N).
vu que l'équilibre s'installe correctement, je pense qu'il s'agit d'un problème de sortie, donc purement informatique. Je remarque par ailleurs que la colonne de "temps" est répétée plusieurs fois. On trouvera le temps en colonne 1, 8, 15 et 20. ça n'a pas l'air d'être un fonctionnement normal.
3) j'ai voulu tester en supprimant contact et frottement. Donc normalement le petit cube ne rencontrera aucun obstacle ni condition limite selon Z et doit donc chercher à traverser le grand cube. A l'évidence, aucun incrément ne devrait converger. Dans les faits, le calcul diverge effectivement rapidement. Mais curieusement, Herezh++ arrive à converger quelques incréments. Dans les fichiers Gmsh et le fichier .maple, on obtient 3 ou 4 incréments en résultat. Les déplacements sont nuls. Et pourtant, par la présence des forces ponctuelles, le résidu ne peut pas être nul. Assez bizarre. ça serait intéressant de voir par quel mécanisme la vérification de convergence est mise en défaut. Je soupçonne que, pour certains incréments, la force ponctuelle n'est plus active (d'où le critère d'arrêt satisfait et les déplacements nuls en résultat). Je ne vois pas d'autre explication.
Dans l'archive jointe, le fichier .info est configuré pour traiter le cas 1) (segmentation fault en présence de contact+frottement). Le fichier .maple fourni correspond au cas 2) (problème sortie force réaction). Je l'ai renommé en exemple_pb_sortie_Freac.maple pour éviter qu'il soit écrasé au lancement du calcul.
C'est peut-être déjà ça qu'il faut regarder. Ensuite, ça peut être intéressant de passer au cas 2) (mise en commentaire de la loi frottement dans "choix_materiaux") pour cette histoire de sortie de résultat. Et enfin, le cas 3), c'est un peu un problème collatéral, voire hors sujet. Pour le traiter, il faut mettre en commentaire tout ce qui est lié au contact (domaine_esclave, loi frottement et para_contact).
a+
Julien
Fichiers
Mis à jour par Gérard Rio il y a environ 3 ans
- Statut changé de Nouveau à En cours
oui, cela ne m'étonne pas car je crois que le frottement de coulomb n'est pas totalement implanté et ....
Mais ça va être l'occasion pour moi de m'y remettre donc je regarde et te tiens au courant, merci pour le test!
Mis à jour par Gérard Rio il y a environ 3 ans
petit détail:
- avec la version non fast, il n'y a pas de segmentation fault mais herezh signale une erreur de dimension -> et s'arrête !donc le résultat est le même mais au moins c'était prévu.
Mis à jour par Gérard Rio il y a environ 3 ans
bon... là ça été rapide, il y avait effectivement un dimensionnement par défaut incorrect.
-> le calcul tourne
Je mets à jour la version osX
Mis à jour par Gérard Rio il y a environ 3 ans
- % réalisé changé de 0 à 40
question 2)
"=> par contre, je n'ai rien en force de réaction sur le grand cube (colonne 11 devrait etre égale à 1 N)."
Le cube 2 est entièrement bloqué. Dans Herezh, lorsque l'on détecte qu'un solide est entièrement bloqué, il ne rentre plus en compte dans les solides déformables pour le contact: il s'agit ici d'un contact déformable - solide rigide. Toutes les informations de réaction, déformations - contraintes, sont dans le solide déformable.
J'ai mis cela en place pour limiter les calculs, car en fait il n'y a pas d'équilibre à rechercher sur le solide 2: il ne sert qu'à imposer des conditions limites au solide déformable 1. Ainsi on peut utiliser un maillage fin pour le solide 2.
Par contre si on bloque uniquement les noeuds de l'embase du solide 2, le problème devient un contact de solides déformable - déformable et là on obtient des réactions sur les noeuds du solide 2.
Donc le comportement observé est normal au sens de la méthodologie que j'ai implantée dans Herezh++
Mis à jour par Julien Troufflard il y a environ 3 ans
Tout d'abord, je rajoute ici ce que tu m'avais dit à l'oral concernant le point 2) : "Je remarque par ailleurs que la colonne de "temps" est répétée plusieurs fois. On trouvera le temps en colonne 1, 8, 15 et 20. ça n'a pas l'air d'être un fonctionnement normal."
=> si si la répétition de la colonne "temps" est un fonctionnement normal (je ne l'avais jamais remarqué)
Ensuite, concernant les forces de réaction :
si je comprends bien, les forces de réactions, c'est la différence entre le vecteur des forces internes (loi de comportement) et ce même vecteur des forces internes auquel on aurait appliqué les conditions limites
=> F_reac = F_int - F_int(CL)
Pour un solide déformable, le contact va provoquer une déformation, donc un effort interne qui équilibrera la force de contact subie par le solide. On récupérerait donc cette force au niveau des forces internes et donc dans F_reac via l'équation précédente.
Mais si pas de déformation => pas de F_int => pas de F_reac
mais dans les faits, il y bien une réaction qui doit se produire sur le solide bloqué. Du coup, est-ce qu'il est envisageable de faire une modif pour transmettre la force de contact au niveau des réactions pour un solide non déformable ?
Mis à jour par Gérard Rio il y a environ 3 ans
- % réalisé changé de 40 à 50
Dans le cas d'un contact rigide-déformable, il n'y a pas de déplacement calculé pour le solide rigide autre que celui imposé. De plus il n'y a pas de couplage entre les deux solides, du au contact: c-a-d que seule la raideur relative au solide déformable, est affecté par le contact, contrairement au cas déformable-déformable pour lequel le contact introduit un couplage entre les deux solides d'où l'importance dans ce cas d'optimiser la largeur de bande.
Ceci étant, dans herezh pour le solide rigide (contrairement à ce que j'ai dit oralement), l'action d'un noeud en contact sur une facette est "bien" reportée sur les noeuds de la facette par extrapolation à l'aide des fonctions d'interpolation. On dispose ainsi d'une répartition de l'action du contact sur le maître (j'avais oublié que j'avais mis cela en place ! )
Pour avoir accès à ces forces on peut indiquer en fin de fichier .info une sortie des fichiers particuliers (voir doc utilisateur)
typiquement dans le cas du test on peut mettre par exemple:
resultats #pas_de_sortie_finale_
COPIE 0
POINTS_INTEGRATION nom_mail= cube_1x1x1 E_tout
Green-Lagrange Almansi Cauchy_global Def_mixte_local Sigma_mixte_local
POINTS_INTEGRATION nom_mail= cube_10x10x1 E_tout
Green-Lagrange Almansi Cauchy_global Def_mixte_local Sigma_mixte_local
fin_point_info ----------Du coup, Herezh génère plusieurs fichiers de résultats et en particulier il y a un fichier .cont qui globalise les infos du contact:
on y trouve (pour l'exemple du test) les réactions aux noeuds esclaves
- Reactions de contact #=====================================================
================= noeud esclave ==================
maillage 1, noeud 4, force = Coordonnee dim= 3 0 0 0.24999996916728079
---------------- noeuds de la frontiere maitre -------------
maillage 2, noeud 5, force = Coordonnee dim= 3 -0 -0 -0.17999997780044219 , de norme =0.17999997780044219
maillage 2, noeud 6, force = Coordonnee dim= 3 -0 -0 -0.019999997533382462 , de norme =0.019999997533382462
maillage 2, noeud 7, force = Coordonnee dim= 3 -0 -0 -0.0049999993833456154 , de norme =0.0049999993833456154
maillage 2, noeud 8, force = Coordonnee dim= 3 -0 -0 -0.044999994450110548 , de norme =0.044999994450110548
================= noeud esclave ==================
maillage 1, noeud 3, force = Coordonnee dim= 3 0 0 0.24999996853110798
---------------- noeuds de la frontiere maitre -------------
maillage 2, noeud 5, force = Coordonnee dim= 3 -0 -0 -0.15999997985990913 , de norme =0.15999997985990913
maillage 2, noeud 6, force = Coordonnee dim= 3 -0 -0 -0.039999994964977269 , de norme =0.039999994964977269
maillage 2, noeud 7, force = Coordonnee dim= 3 -0 -0 -0.0099999987412443137 , de norme =0.0099999987412443137
maillage 2, noeud 8, force = Coordonnee dim= 3 -0 -0 -0.039999994964977269 , de norme =0.039999994964977269
================= noeud esclave ==================
maillage 1, noeud 2, force = Coordonnee dim= 3 0 0 0.24999996916733888
---------------- noeuds de la frontiere maitre -------------
maillage 2, noeud 5, force = Coordonnee dim= 3 -0 -0 -0.17999997780048402 , de norme =0.17999997780048402
maillage 2, noeud 6, force = Coordonnee dim= 3 -0 -0 -0.044999994450121004 , de norme =0.044999994450121004
maillage 2, noeud 7, force = Coordonnee dim= 3 -0 -0 -0.0049999993833467768 , de norme =0.0049999993833467768
maillage 2, noeud 8, force = Coordonnee dim= 3 -0 -0 -0.019999997533387107 , de norme =0.019999997533387107
================= noeud esclave ==================
maillage 1, noeud 1, force = Coordonnee dim= 3 0 0 0.24999996916716472
---------------- noeuds de la frontiere maitre -------------
maillage 2, noeud 5, force = Coordonnee dim= 3 -0 -0 -0.20249997502540343 , de norme =0.20249997502540343
maillage 2, noeud 6, force = Coordonnee dim= 3 -0 -0 -0.02249999722504482 , de norme =0.02249999722504482
maillage 2, noeud 7, force = Coordonnee dim= 3 -0 -0 -0.0024999996916716459 , de norme =0.0024999996916716459
maillage 2, noeud 8, force = Coordonnee dim= 3 -0 -0 -0.02249999722504482 , de norme =0.02249999722504482
Là il s'agit sur les noeuds de la facette maître, de l'extrapolation du noeud esclave qui est en contact.
Par contre chaque contact étant géré dans Herezh par un couple noeud esclave + facette maître, un noeud facette peut appartenir à plusieurs éléments de contact. Du coup actuellement pour un noeud facette il faut faire la somme de toutes les extrapolations pour avoir la globalité des actions de contact sur le maître. A priori cela ne pose pas de pb car il y a toutes les données disponibles, mais il faut le rajouter à la suite d'Herezh.
Enfin, normalement sur chaque noeud maître, pendant le calcul du contact, le cumul de la force de contact est "bien" également reporté sur les réactions !!! mais en sortie on a 0. ! là il y a un fct qui m'échappe pour l'instant donc... affaire à suivre !
Mis à jour par Julien Troufflard il y a environ 3 ans
"""
Enfin, normalement sur chaque noeud maître, pendant le calcul du contact, le cumul de la force de contact est "bien" également reporté sur les réactions !!! mais en sortie on a 0. ! là il y a un fct qui m'échappe pour l'instant donc... affaire à suivre !
"""
=> c'est bon signe pour avoir ces valeurs en sortie .maple alors!!
concernant les valeurs obtenues dans le fichier .cont, je confirme qu'elles sont bonnes. Comme ce fichier n'est créé que pour le dernier incrément, j'ai regardé ce fichier en étudiant chaque step du calcul. Le cube "esclave" se déplace en 2 temps.
=> Au step 1, il ne se déplace que selon Z. Pour ce step, le cumul des forces Z reportée au noeud 5 maillage 2 (maitre) du fichier .cont est égale à -0.722996. Sachant qu'il faut obtenir une force de réaction de l'ordre de +0.7225 pour ce noeud.
=> Au step 2, il se déplace un peu selon Y. Dans ce cas, Herezh donne -0.714915 sachant qu'il faut obtenir une réaction de +0.714.
S'il est possible de transférer ces valeurs vers le .maple pour les avoir à chaque incrément, c'est tout bon pour cette partie!!
par contre, je ne sais pas trop comment il faut gérer le cas entre un solide maitre déformable et un solide maitre non déformable. De ce que je sais, si tous les noeuds du maitre sont bloqués, il n'y a aucune force de réaction sur les noeuds non concernés par une surface de contact (dans le cas présent, les noeuds du bas du cube 10x10x1 n°1, 2, 3 et 4 devraient avoir une force de réaction nulle, tandis que les noeuds du haut auront une force de réaction non nulle et de valeurs variables selon leur position par rapport au contact). Mais dans le cas où le solide maitre est déformable, il ne va pas falloir superposer les réactions "naturelles" liées à la déformation et les réactions venant des facettes en contact. Et donc que j'imagine que les CL devraient permettre de faire la part des choses.
pour la suite du ticket, concernant le frottement, le bug initial est bien résolu (le calcul va jusqu'à la fin). Mais je n'obtiens pas à l'heure actuelle de force de réaction sur le cube 1x1 (colonne 3 du .maple). Il doit récupérer normalement une force de réaction totale selon y de +0.1. Et je mets bien un signe +. Car il y a une erreur dans mon tout premier message du ticket. J'ai dit :
"
2) dans le second step => toujours 1 N selon Z sur le grand cube + il faut obtenir une force de réaction sur le petit cube de -0.1 N selon Y (colonne 3 du .maple)
"
mais la force de -0.1 c'est la force de frottement, et donc on doit récupérer l'équivalent en sens opposé +0.1 en réaction.
Mis à jour par Gérard Rio il y a environ 3 ans
- % réalisé changé de 50 à 80
Concernant l'accès aux forces de réactions sur un solide rigide du à un contact via un solide déformable :
1) l'accès est en fait possible au travers de 2 ddl_etendu qui ont été mis en place justement pour cela !
reaction_normale -> la réaction normale
reaction_tangentielle -> donne la réaction tangentielle
- là on obtient la valeur totale cumulée de l'action du contact sur chaque noeud de la facette
- il s'agit d'un sous-produit de l'équilibre. Les réactions sont calculées par extrapolation des forces de contact créées par les noeuds esclaves sur les facettes maîtres.
2) les réactions R_Xi sont à 0 car elles proviennent directement de la résolution, qui (comme expliqué précédemment dans le post) est associée aux ddl directement mis en cause. Or, le solide maître étant complètement bloqué, les ddl sont bloqué, il ne se déforme pas : au niveau de la MMC, je n'ai pas de réaction associé.
Donc en résumé: les R_Xi ne représentent pas toujours la même chose que les "reaction_normale" et tangentielle de contact, cela dépend du statuts des solides en présence.
Il y a surement d'autre manière de traité la chose. L'intérêt de mon choix est de pouvoir actuellement utiliser séparément c'est deux grandeurs. Mais il faut effectivement avoir en tête la signification de chaque grandeur.
Je vais préciser cela dans la doc.
Mis à jour par Julien Troufflard il y a environ 3 ans
oui, effectivement, on obtient l'ensemble des forces dans reaction_normale et reaction_tangentielle. J'ai également regardé les grandeurs évoluées VECT_REAC_N et FORCE_CONTACT.
bon, c'est bien compliqué tout ça et la suite est dense. En résumé, j'ai l'impression que toutes les infos sont là mais il faut savoir ce que l'on fait en fonction de cas précis de calcul.
je vais écrire ici ce que j'ai constaté sur ce cas test et ensuite je vais passer à un cas qui m'intéresse très concrètement et voir si c'est ok pour calculer ce que je veux en l'état (à savoir une contrainte nominale selon y d'un calcul axi avec du frottement, et donc pour ça il faut que je récupère une somme de réaction quelque part)
il y a 3 aspects qui m'apparaissent important dans les résultats :
- les valeurs et leur signe
- le ddl concerné par telle ou telle valeur (X Y ou Z)
- si je veux calculer une somme de forces sur une liste de noeuds, où faut-il récupérer les infos pour ne rien oublier
concernant les grandeurs reaction_normale et reaction_tangentielle :
je vois bien que les valeurs sont grosso modo conformes à ce qu'il faut obtenir (pour chaque noeud de chaque cube c'est ok). ça permet d'ailleurs de voir que le frottement est bien effectif (0.1 N au global en tangentiel et la répartition par noeud du maitre est également bonne). Donc déjà on écrit en gros ce premier bon point :) => LE FROTTEMENT FONCTIONNE.
Pour aller plus loin, il manque la répartition par composante (x y ou z) et le signe. On dispose seulement d'une norme. Concernant reaction_normale, il est possible de combiner avec la grandeur évoluée NORMALE_CONTACT pour repartir cette norme sur chaque direction de l'espace.
Je n'ai pas trouvé l'équivalent pour répartir la partie tangentielle.
En résumé, voici les points qui ne permettent pas d'utiliser reaction_normale et reaction_tangentielle les yeux fermés :
1) on obtient des reaction_normale (donc selon z) sur le cube esclave alors qu'aucun noeud de ce maillage n'est bloqué selon z
2) la grandeur NORMALE_CONTACT n'est pas dispo aux noeuds du maitre (valeurs nulles). Donc, on ne peut pas répartir reaction_normale dans l'espace pour le cube maitre (c'est pourtant lui qui est sensé exprimer une réaction selon z)
3) je n'ai pas trouvé l'équivalent de NORMALE_CONTACT pour répartir dans l'espace la partie tangentielle reaction_tangentielle
4) dans ce cas test, on sait que la partie tangentielle est selon y, donc les valeurs reaction_tangentielle sont bonnes. Reste à savoir si le signe des composantes sera correct après application d'un vecteur de répartition de cette norme. SACHANT QUE : le cube esclave est sensé récupéré une réaction positive (+0.1 N) tandis que le maitre doit récupérer la même en sens opposé (-0.1 N)
Concernant les grandeurs VECT_REAC_N et FORCE_CONTACT, voici les constats :
1) intéressant car ce sont des vecteurs (donc déjà répartis en composantes). Le frottement est inclus dans ces grandeurs
2) les 2 grandeurs donnent les mêmes résultats, c'est-à-dire de même signe. C'est peut-être étrange étant donné que l'un est une réaction et l'autre une force de contact. Mais c'est peut-être moi qui ne comprend pas s'il y a une différence ou non entre réaction et contact (ça dépend du point de vue selon les cubes).
3) comme pour NORMALE_CONTACT, les valeurs sont nulles sur le maitre et non nulles sur l'esclave (devrait être l'inverse pour les réactions)
4) on récupère bien le frottement sur l'esclave, mais du coup le signe est négatif (composante y devrait être positive pour VECT_REAC_N sur l'esclave)
bon, je retiens surtout que le frottement marche. Comme dis précédemment, je vais passer un cas plus concret axisymétrique.
Mis à jour par Gérard Rio il y a environ 3 ans
" => LE FROTTEMENT FONCTIONNE."
pas tout à fait, car pour l'instant il n'y a que la partie dans le cône de Coulomb, il faut que j'ajoute le fait de glisser à force de frottement constant...mais effectivement tant que l'on n'a pas atteint la limite de glissement l'implantation actuelle est correcte (au bug près)
"En résumé, voici les points qui ne permettent pas d'utiliser reaction_normale et reaction_tangentielle les yeux fermés :
1) on obtient des reaction_normale (donc selon z) sur le cube esclave alors qu'aucun noeud de ce maillage n'est bloqué selon z "
je ne sais pas si je comprends bien, mais si tu demandes un ddl en sortie, Herezh sort systématiquement une valeur, 0. s'il n'y a rien de stocké (c'est en général vrai (!) pour tous les ddl).
Par contre les grandeurs "NOEUD_PROJECTILE_EN_CONTACT" et "NOEUD_FACETTE_EN_CONTACT" pour chaque noeud, permettent de savoir (cf. doc)
- si un noeud est considéré comme un noeud projectile (esclave) dans un élément de contact actif
- "et/ou" si le noeud appartient à une facette en contact active
" 2) la grandeur NORMALE_CONTACT n'est pas dispo aux noeuds du maitre (valeurs nulles). Donc, on ne peut pas répartir reaction_normale dans l'espace pour le cube maitre (c'est pourtant lui qui est sensé exprimer une réaction selon z)"
oui, c'est voulu, car la normale au point de contact est calculée via l'interpolation de la facette. Du coup si un noeud facette par exemple, appartient à deux éléments on obtiendrait 2 normales ! a priori différentes.
Dans le cas d'une surface 2D, on peut récupérer la normale moyennée aux noeuds aux différents temps via "NN_SURF_t0", "NN_SURF_t" et "NN_SURF"
On pourrait imaginer faire la même chose pour les frontières 2D des éléments 3D de contact. Une solution actuelle est peut-être de coller une surface sur les éléments 3D, et de récupérer les normales de cette surface (?)
"3) je n'ai pas trouvé l'équivalent de NORMALE_CONTACT pour répartir dans l'espace la partie tangentielle reaction_tangentielle"
oui
en fait on a les infos pour calculer, on a (cf. code ElContact_2.cc méthode: ElContact::SM_K_charge_contact() par exemple, du côté de la ligne 816 (sur ma version) ) :
dep_tangentiel = M_tatdt- N * (M_tatdt*N); // on retire le deplacement normal éventuelOn pourrait imaginer de construire et stocker un vecteur normé selon dep_tangentiel
"4) dans ce cas test, on sait que la partie tangentielle est selon y, donc les valeurs reaction_tangentielle sont bonnes. Reste à savoir si le signe des composantes sera correct après application d'un vecteur de répartition de cette norme. SACHANT QUE : le cube esclave est sensé récupéré une réaction positive (+0.1 N) tandis que le maitre doit récupérer la même en sens opposé (-0.1 N)"
c'est toujours un pb les signes, car cela dépend de quel point de vue on se place. Ceci étend c'est toujours le même pt de vue qui est utilisé ! donc une fois que l'on a le type de fct on peut l'appliquer pour tout calcul.
*"Concernant les grandeurs VECT_REAC_N et FORCE_CONTACT, voici les constats :
1) intéressant, car ce sont des vecteurs (donc déjà répartis en composantes). Le frottement est inclus dans ces grandeurs"
*
oui mais il faut avoir en tête que ces vecteurs globalisent toutes les réactions et toutes les forces de contact
"2) les 2 grandeurs donnent les mêmes résultats, c'est-à-dire de même signe. C'est peut-être étrange étant donné que l'un est une réaction et l'autre une force de contact. Mais c'est peut-être moi qui ne comprend pas s'il y a une différence ou non entre réaction et contact (ça dépend du point de vue selon les cubes)."
oui, les signes (cf. précédente remarque) !!
"3) comme pour NORMALE_CONTACT, les valeurs sont nulles sur le maitre et non nulles sur l'esclave (devrait être l'inverse pour les réactions)"
c'est logique vu les remarques précédentes
"4) on récupère bien le frottement sur l'esclave, mais du coup le signe est négatif (composante y devrait être positive pour VECT_REAC_N sur l'esclave)"
toujours les signes !
Mis à jour par Julien Troufflard il y a environ 3 ans
- Fichier influence_frottement.png influence_frottement.png ajouté
- Fichier diff_reaction_haut_bas.png diff_reaction_haut_bas.png ajouté
- Fichier frottement_axi.tar frottement_axi.tar ajouté
" => LE FROTTEMENT FONCTIONNE."
pas tout à fait, car pour l'instant il n'y a que la partie dans le cône de Coulomb, il faut que j'ajoute le fait de glisser à force de
frottement constant...mais effectivement tant que l'on n'a pas atteint la limite de glissement l'implantation actuelle est correcte
(au bug près)
ah ok, je croyais que le test en déplacement imposé montrait qu'il était capable de glisser tout en donnant la bonne force. Mais effectivement, le dernier test que je viens de faire montre bien qu'il y a un souci de comportement du frottement.
J'ai mis en place un test axisymétrique très simple (un écrasement de cylindre, en contact avec un maillage non déformable). Je joins ce test à ce message. Le readme explique bien (oscillation de la force de reaction pour un fort coef de frottement, dépendance au maillage : plus le maillage est fin, plus le coef de frottement doit être petit si on veut éviter le bug)
je mets ici les courbes obtenues en terme d'écrasement-contrainte nominale
1) influence du frottement sur la reaction en bas du maillage déformable (oscillation pour un grand coef de frottement) :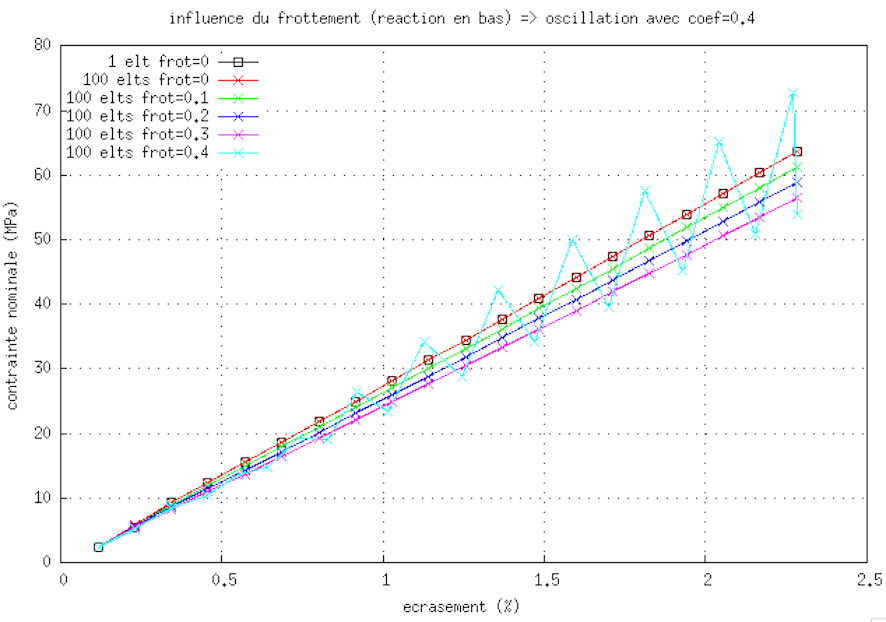
2) différence de réaction récupérée en haut (noeuds N_N, lieu d'application du déplacement imposé) et en bas (noeuds N_S, noeuds bloqués) :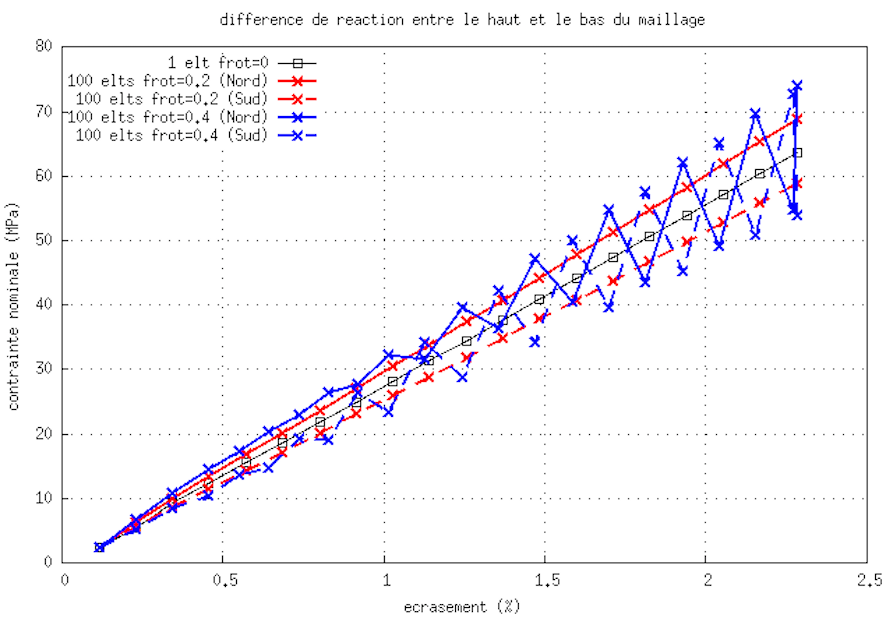
donc à suivre pour ce test selon la suite de l'implantation du frottement...
pour ce qui est des grandeurs de sortie, je ne sais pas trop quoi dire ou proposer. Les implantations sont très certainement logiques. Pour ma part, j'obtiens (je crois) ce que je veux dans le cas précis axisymétrique que j'envisage et qui est très proche du cas test joint à ce message. Parce que tout simplement, je récupère un torseur de réaction sur un solide déformable.
Mis à jour par Julien Troufflard il y a environ 3 ans
- Fichier influence_emaxi_ecrasement_contrainte.png influence_emaxi_ecrasement_contrainte.png ajouté
- Fichier influence_emaxi_Uy_reaction.png influence_emaxi_Uy_reaction.png ajouté
pour compléter le cas test AXI précédent, j'ai constaté un truc intéressant, en espérant que ça donne une piste pour débugger.
Lors de mon dernier message, je montrais que le résultat était sensible à la taille d'éléments. Mais pour un même maillage, on retrouve ce même phénomène si on passe e_maxi (PENETRATION_CONTACT_MAXI) à 1e-4 au lieu de 1e-7. Les noeuds en contact voient leur déplacement osciller.
J'ai fait le test avec le maillage 100 éléments et coef frottement 0.3.
Voici les graphes
1) écrasement - contrainte nominale (calculée avec la réaction selon Y sur N_S) :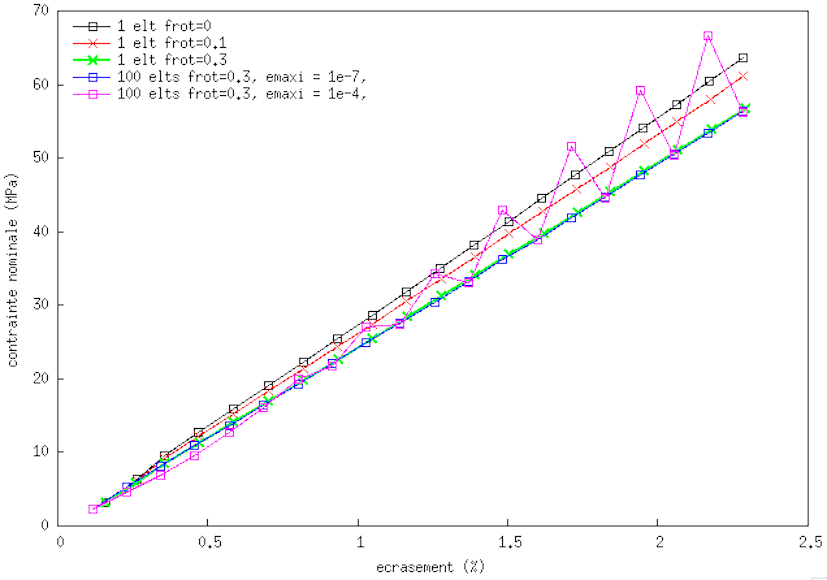
=> pour e_maxi=1e-7, la solution 100 éléments est calée sur la solution 1 élément. Sinon pour e_maxi=1e-4, il y une oscillation avec un incrément sur deux calé sur la "bonne solution".
2) n°incrément versus déplacement Uy d'un noeud en contact (noeud 117, soit à peu près au milieu de l'arête Est du maillage déformable) et réaction totale y sur N_S :
=> l'oscillation de réaction est liée à une oscillation du déplacement (tous les noeuds N_E oscillent de cette manière, sauf le noeud bloqué en N_S).
Donc, la réaction obtenue oscille de manière synchrone avec l'oscillation du déplacement.
On a sans arrêt l'enchainement suivant sur les noeuds N_E :
1) un noeud atteint un certain UY à un incrément i et ce UY est "correct" par comparaison avec le calcul sans oscillation (de même pour la réaction totale du système)
2) ce noeud rebrousse chemin selon y à l'incrément i+1 affectant la réaction du système
Mis à jour par Julien Troufflard il y a environ 3 ans
le graphe 2 n'est pas passé dans mon message précédent. Le voici :
2) n°incrément versus déplacement Uy d'un noeud en contact (noeud 117, soit à peu près au milieu de l'arête Est du maillage déformable) et réaction totale y sur N_S :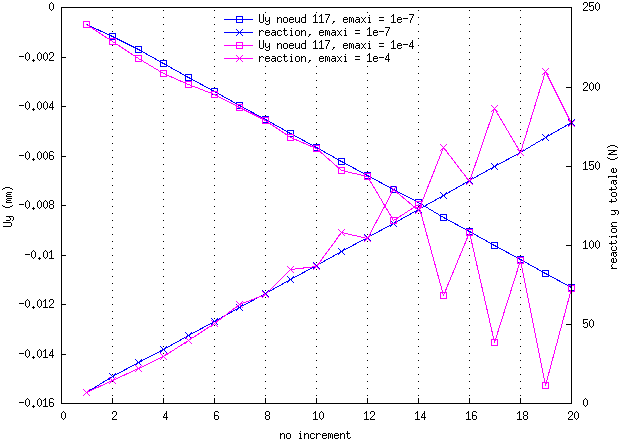
Mis à jour par Gérard Rio il y a environ 3 ans
après re...re... relecture de ce que j'ai implanté... et bien si, j'ai bien tout implanté !! a priori coulomb est complet. (la doc théorique ne semble pas terminée )
Bon... cela ne veut pas dire que tout est ok !!, en particulier je ne comprends pas trop les oscillations pour l'instant
je continue à cogiter
Merci Julien pour tes investigations !
Mis à jour par Gérard Rio il y a environ 3 ans
j'ai mis à jour la documentation théorique concernant des aspects du calcul du frottement de coulomb.
à suivre ...