Anomalie #346
ouvertloi ISOHYPER3DORGEAS2 : dépendance à Lode sur alpha1
Description
Gérard,
dans la loi ISOHYPER3DORGEAS2, le paramètre alpha1 n'est pas dépendant de Lode. Actuellement, on dirait que seul Qs, mu1, mu2, mu3 et Qe peuvent dépendre de Lode.
Serait-il possible de rendre accessible une dépendance à Lode pour alpha1 (et alpha2 ?) ?
J'ai mis en pièce jointe un calcul de traction avec tout ce qu'il faut pour une dépendance à Lode de alpha1 (en supposant que le mot-clé serait alpha01_phi= ).
Les lois d'évolution COURBEPOLYNOMIALE sont des droites (premier coef est l'ordonnée à l'origine, second est le coef directeur)
Autre question : je ne sais pas comment placer le mot-clé "" avec_regularisation_ "" pour la loi ISOHYPER3DORGEAS2. La doc dit de mettre ce paramètre après tous les autres. J'ai essayé divers endroits sans succès, avec ou sans symbole de continuation de ligne. (je l'ai mis en commentaire)
Autre question par curiosité : dans la loi du calcul pièce jointe, si on garde tel quel les coefficients mais que l'on met dans alpha1 0.03 au lieu de 0.01, le calcul diverge. Pourtant, 0.03 est une valeur classique. J'aimerais comprendre pourquoi, au cas où je rencontre ce problème un jour.
merci d'avance,
Julien
Fichiers
Mis à jour par Julien Troufflard il y a plus de 2 ans
ps : concernant ma dernière question, je pense que le problème de divergence avec alpha1=0.03 disparaitra avec le paramètre de régularisation. Si on augmente le pas de temps, le calcul passe. ça veut donc bien dire que c'est un problème de EPS trop petite pour calculer la phase.
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier loi_test.hz_loi loi_test.hz_loi ajouté
Gérard,
ci-joint une nouvelle version du fichier loi de comportement.
J'ai réussi à placer le mot-clé avec_regularisation_
Le calcul se lance correctement (et converge si tu passes le pas de temps à 0.05 par exemple).
Par contre, la valeur de régularisation n'a aucune influence. J'ai toujours le même résultat (fichier gnu) que je mette 1e-5, 1e-1 ou même 1.
Mis à jour par Gérard Rio il y a plus de 2 ans
- Statut changé de Nouveau à En cours
"Serait-il possible de rendre accessible une dépendance à Lode pour alpha1 (et alpha2 ?) ?"
oui, cf. ce que l'on a vu en formation. Méthode:
- faire comme dans le cas des autres paramètres à l'aide d'une fonction nD
NB: la dépendance de l'angle de phase aux ne sera pas prise en compte de cette manière. Une solution plus complète serait d'utiliser une fonction nD (ou une courbe 1D) qui ramènerait la valeur et ses dérivées première seconde, et d'introduire (après un calcul analytique) ces dérivées dans le calcul de l'opérateur tangent
Mis à jour par Gérard Rio il y a plus de 2 ans
- % réalisé changé de 0 à 40
Autre question : je ne sais pas comment placer le mot-clé "" avec_regularisation_ "" pour la loi ISOHYPER3DORGEAS2. La doc dit de mettre ce paramètre après tous les autres. J'ai essayé divers endroits sans succès, avec ou sans symbole de continuation de ligne. (je l'ai mis en commentaire)
la lecture n'était pas correcte, on lisait jusqu'au mot clé "fin_parametres_avec_phase_" mais ce mot clé n'était pas lue également dans le flux, on testait seulement son existence, du coup à la lecture suivante le mot clé "avec_regularisation_" n'était pas correctement lu...
cf. les nouvelles sources consultables sous git.
J'ai corrigé et testé sur ton cas... a priori cela fonctionne (peux-tu vérifier ?)
C'est mis à jour dans la version 7.014
Mis à jour par Gérard Rio il y a plus de 2 ans
- % réalisé changé de 40 à 50
Autre question par curiosité : dans la loi du calcul pièce jointe, si on garde tel quel les coefficients mais que l'on met dans alpha1 0.03 au lieu de 0.01, le calcul diverge. Pourtant, 0.03 est une valeur classique. J'aimerais comprendre pourquoi, au cas où je rencontre ce problème un jour.
Avec l'utilisation de la version non fast, on voit que c'est l'algorithme de contrainte plane qui ne converge pas.
Avant de regarder les paramètres de cet algo, je pense qu'il faut regarder sur un essai de traction simple la forme de l'évolution de la loi en fonction d'alpha1 et en particulier, ce qu'il en est pour la valeur 0.03
Je vois que tu utilises un Qs de 1 , peut-être que c'est incompatible avec un alpha grand ? (le Qs donne la hauteur du premier palier). Mais je n'ai pas vraiment d'idée. Je pense que c'est peut-être d'abord un pb de mécanique avant d'être un disfonctionnement informatique.
Par exemple avec Qs = 4 et alpha1 = 0.03 cela fonctionne mais avec Qs = 2 cela ne fonctionne pas donc je ne serais pas étonné qu'il y ait une valeur limite de Qs en fonction de alpha1 qui en fait gère la courbure de l'évolution de la contrainte. Mais c'est juste une piste.
à tester...
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier pb_ISOHYPER3DORGEAS2.tar pb_ISOHYPER3DORGEAS2.tar ajouté
ok pour la divergence avec certaines valeurs de alpha1.
concernant les 2 autres points :
1) dependance a cos(3phi) sur alpha1 :
il manque juste un mot pour comprendre ce que tu as mis dans le "NB" (NB: la dépendance de l'angle de phase aux ne sera pas prise...). Je crois comprendre qu'il est question de l'opérateur tangent. Ce point est très important dans le cas d'une loi contrainte plane. Quel est le fonctionnement de Herezh selon les cas (courbe1d et fonction nD) ?
- dans le cas d une dependance a COURBE1D : est-ce que la dérivée est prise en compte dans l'opérateur tangent ?
- dans le cas courbe nD : veux-tu dire que la dérivée n'est pas prise en compte ?
quelle que soit l'approche, si la variation n'est pas prise en compte, je serai obligé d'abandonner cette solution (le risque de divergence sera trop grand dans un modèle à N points d'intégration sollicités de manière diverses au cours de milliers d'itérations).
2) j'ai encore des pb de divergence et de prise en compte de "avec_regularisation_"
j'ai remanié les paramètres de l'exemple. En gros, dans la nouvelle loi de l'archive pièce jointe, les coefs initiaux sont sensés être ceux dans le cas cos(3phi)=1 (traction uniaxiale). Cette loi a l'air de tourner en traction uniaxiale.
Par contre, dans l'archive pièce jointe, j'ai ajouté une condition limite selon UY (même chargement que selon UX). Il s'agit d'une traction biaxiale. Et là, la loi ne converge pas en petite déformation => contrainte infinie au départ. Le reste du calcul a l'air de tourner. Par contre, le paramètre "avec_regularisation_" n'a aucune influence.
J'ai essayé divers mot-clés pour essayer de voir quels étaient les paramètres utilisés par Herezh (valeur de cos(3phi) et valeur des coef) mais je n'ai toujours pas compris comment utiliser les mots-clés permet_affichage et sortie_post. J'ai essayé de regarder dans le .BI, etc...
ps : ne pas tenir compte du fichier gnu_coef. Il me sert à piffométrer des paramètres de dépendance à la phase
a+
Julien
Mis à jour par Gérard Rio il y a plus de 2 ans
1) dans le cas d une dependance a COURBE1D : est-ce que la dérivée est prise en compte dans l'opérateur tangent ?
oui, il suffit de regarder les sources (ex: ligne 2192 à 2215 : méthode Hyper3D::PoGrenobleAvecPhaseAvecVar IsoHyper3DOrgeas2::PoGrenoblePhase_et_var
(const Invariant2QepsCosphi& i_s,const Invariant & inv))
dans le cas courbe nD : veux-tu dire que la dérivée n'est pas prise en compte ?
oui
quelle que soit l'approche, si la variation n'est pas prise en compte, je serai obligé d'abandonner cette solution (le risque de divergence sera trop grand dans un modèle à N points d'intégration sollicités de manière diverses au cours de milliers d'itérations).
ah mon pauvre: qui ne risque rien n'a rien !
2) je crois qu'il faudrait (comme je te l'ai suggéré) essayer de regarder la convexité de la loi ou au moins en avoir une idée. Il y a une petite réflexion théorique à mener mais quelque soit la loi d'hyperélasticité, cela me paraît un passage obligé pour répondre aux questions unicité de solution.
Ce type de loi est très flexible mais la contrepartie est l'absence de convexité possible. Du coup on peut très bien avoir plusieurs solutions pour un état de chargement (ce qui est également possible physiquement) et la conduite de la convergence est alors délicate mais pas impossible: par exemple dans les algo de Newton en limitant l'incrément à chaque itération ...(cf. l'algo général en implicite).
Je vais regarder la fin dès que possible
Mis à jour par Julien Troufflard il y a plus de 2 ans
quelle que soit l'approche, si la variation n'est pas prise en compte, je serai obligé d'abandonner cette solution (le risque de divergence sera trop grand dans un modèle à N points d'intégration sollicités de manière diverses au cours de milliers d'itérations).
ah mon pauvre: qui ne risque rien n'a rien !
pffff... c'est pas le propos d'être fringant ou pas. Le contexte est une loi qui va se faire embarquer dans une loi contrainte plane dans des calculs longs de relaxation dynamique. Si je propose une loi dont l'opérateur tangent est défaillant, c'est très mal parti. Le controle sur l'algo Newton contrainte plane est très limité, les calculs vont planter/stagner des fois oui des fois non, possiblement n'importe où dans le maillage (idéalement après une nuit de calcul). Cette loi combine la flexibilité aux diverses possibilités de trajet tout en étant compatible critère pli. Si elle est ok, je vais l'utiliser tout le temps et elle va se retrouver dans plein d'application (utilisateur aguerri ou calcul boite noire).
Je comprends bien les histoires de convexité, mais d'un certain côté, les paramètres que j'ai à rentrer sont ceux qui permettent de fitter une courbe. Et donc convexité ou pas, ce sont bien ces paramètres que je suis obligé de mettre. Le tout asservi par une relation linéaire dans la dépendance à Lode, ça me parait assez soft et le moins propice à surprises. D'ailleurs, j'avais abandonné cette solution quand j'avais testé l'autre version ISOHYPER3DORGEAS1. Pour le coup, même avec des tests simples, la convergence était difficile. Jamais avec cette version 2 + dépendance linéaire. Une fois le problème petite déformation réglé (régularisation), ça sera pas mal.
D'un autre côté, de mémoire, le coefficient alpha n'est pas le coef le plus critique. Je vais voir ce que ça donne pour l'instant en mettant un coef alpha constant.
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier pb_ISOHYPER3DORGEAS2.tar pb_ISOHYPER3DORGEAS2.tar ajouté
2 choses sur cette loi :
- tout se passe normalement si on fait une loi des mélanges de manière à éviter la dépendance à la phase en petite déformation (pas de contrainte infinie en début de courbe). Il y a donc bien un problème de lecture et/ou d'application du paramètre de régularisation.
- j'ai testé par curiosité le cas d'une dépendance à la phase sur alpha1 avec une fonction nD. Mais Herezh me renvoie une erreur à la lecture du .info. Comme dans le cas d'une courbe 1D classique, on dirait que l'utilisation d'une fonction nD n'est permise que sur les paramètres Qs, mu1, mu2, mu3, Qe. Erreur Herezh :
erreur en lecture de la dependance a une fonction nD des coefficients, on aurait du lire le mot cle mu01_nD= ou mu02_nD= ou mu03_nD ou Q0s_nD= ou Q0e_nD= et on a lue: alpha01_nD=
j'ai essayé en mettant : "alpha01_nD=" et en mettant "alpha1_nD="
J'ai également regardé le code source et je ne vois nulle part la modification de alpha1 via une courbe nD.
En pièce jointe, j'ai mis un second matériau dans le fichier "loi_test.hz_loi" de nom "MAT_nD". Il s'agit d'une loi où seul alpha1 dépendrait de la phase via une fonction nD (variant linéairement entre 0.03 en compression uniaxiale à 0.04 en traction uniaxiale). Dans le fichier .info, j'ai ajouté la fonction nD "fct_alpha1".
NB : dans le fichier "loi_test.hz_loi", j'ai également mis une loi MAT_nD_TousLesParam qui regrouperait toutes les dépendances courbe 1D "avec_phase" avec celle sur alpha01 en fonction nD (si on veut, ça serait la loi finale à faire fonctionner)
a+
Julien
Mis à jour par Gérard Rio il y a plus de 2 ans
- % réalisé changé de 50 à 60
Comme vue pendant la formation (cf. IsoHyper3DOrgeas2.h) les paramètres qui peuvent être dépendants soit d'une fonction nD soit de la phase sont:
//variables utilisées dans le cas d'une dépendance à la phase
Courbe1D* mu01_phi, * mu02_phi, mu03_phi;
Courbe1D Q0s_phi, * Q0e_phi;
// cas d'une dépendance à une fonction nD
Fonction_nD* mu01_nD, * mu02_nD, mu03_nD;
Fonction_nD Q0s_nD, * Q0e_nD;Les paramètres alpha1 et alpha3 qui règlent les courbures, sont fixes d'où l'erreur en lecture d'Herezh.
Je vais compléter la doc à ce sujet.
Comme je l'ai dit dans ma réponse #2, Il est possible d'introduire une dépendance des coef alphi, à la phase via une courbe qui intègre une dérivée première et seconde, ce qui permettrait de l'introduire dans l'opérateur tangent. Il faut tout d'abord rédiger la partie théorique associée.
Mis à jour par Julien Troufflard il y a plus de 2 ans
vu.
Pour l'instant, je suis très embêté par la partie régularisation. Je contourne cette partie qui ne fonctionne pas encore par une loi des mélanges. ça fonctionne sur certains cas. Mais en fait, c'est très dépendant du pas de temps. Si le pas de temps initial du calcul est assez petit, j'ai des calculs très simples (traction uniaxiale, un seul élément) qui ne convergent pas en contrainte plane. Si je l'augmente, ça passe.
J'ai rien pour le confirmer mais je soupçonne un problème d'opérateur tangent au point de basculement entre une loi 1 sans phase à une loi 2 avec phase (la loi de mélange ne prend pas en compte la fonction de mélange dans le calcul des dérivées). C'est vraiment un point critique en contrainte plane.
Je vais essayer avec une transition smooth pour voir (fonction 1-cos)
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier loi_Orgeas1.hz_loi loi_Orgeas1.hz_loi ajouté
bizarre bizarre au sujet de la régularisation.
Je n'avais pas percuté que dans mon cas particulier de dépendance à la phase (fonction linéaire sur Qs,mu1,mu2), il se trouve que je peux me contenter de Orgéas 1 (il suffit de mettre n=-1 et trouver les bons paramètres 0 et gamma). Je peux donc reproduire ma loi Orgéas 2 avec Orgéas 1.
Avec cette loi Orgéas 1, je n'ai pas de bug au départ (ci-joint la loi Orgéas 1 de nom MAT_o1). Toujours avec cette loi, je m'aperçois qu'en modifiant le param de régularisation, je n'ai pas non plus d'influence sur mon résultat. Donc en apparence, une régularisation qui ne fonctionnerait pas, comme Orgéas 2.
Mais en fait, en calculant moi-même l'angle de Lode en fonction de la régularisation, je m'aperçois que la valeur de l'angle de Lode n'est pas si sensible que ça au paramètre de régularisation, à moins de mettre une valeur très grande peut-être. à approfondir, c'était du vite fait pour voir...
En parcourant les sources Herezh, on voit bien que la fonction qui calcule la phase vient de la classe parent Hyper3D, donc idem pour Orgéas 1 et Orgéas 2.
J'en arrive à me dire que le pb sur Orgéas 2 ne viendrait pas de la régularisation (malgré le fait que le pb apparait en petite déformation). Difficile de comprendre le code source sans pouvoir le compiler. En comparant les .h et .cc de ces 2 lois, on voit juste qu'il y a quelques "ORGEAS1" qui apparaissent dans les fichiers de Orgéas 2 (mais ça ne concerne que des affichages dans le terminal).
Mis à jour par Gérard Rio il y a plus de 2 ans
La régularisation intervient dans hyper3D sur le calcul des invariants et est ainsi indépendante du potentiel. Donc à ce niveau, la réponse doit-être identique entre orgeas1 et orgeas2.
Par contre la forme de dépendance du potentiel à la phase est différente entre les deux lois.
D'une manière générale si on utilise une régularisation, normalement l'idée est de ne pas utiliser une transition entre deux lois (une sans phase au début et une avec phase après).
Et si on utilise une transition, il la régularisation est peut-être surabondant.
J'ai déjà eu le type de pb que tu observes.
- pour les potentiels (que j'appelle de Grenoble, car issu d'équipes de recherche de Grenoble) il y a souvent un risque pb lorsque l'intensité est très faible et que l'on utilise la phase.
- l'utilisation d'une loi des mélanges est une solution possible
- l'utilisation de la régularisation est une autre solution
Mais l'influence de la taille des premiers pas de charge à toujours une importance prédominante.
Dans mes calculs j'ai toujours réussi à trouver un pas ad hoc, mais souvent il m'a fallu tâtonner pour trouver un bon démarrage.
Ceci étant, j'ai souvent préféré utiliser orgeas1, pour lequel je pouvais facilement contrôler la convexité contrairement à orgeas2.
J'ai développé orgeas2 pour étendre les possibilités d'évolution de paramètres. Par contre comme dit précédemment on peut très bien obtenir alors des potentiels non convexes et donc dans ce cas plusieurs solutions possibles pour une même intensité de chargement.
Il faut alors piloter le passage de ces points à solution multiple ce qui rajoute en complexité.
NB: pour info il y a aussi un coeff défini en dur toujours dans Hyper3D, qui intervient dans les calculs initiaux:
double Hyper3D::limite_inf_bIIb = 36.e-10; // limite en dessous de laquelle on fait une ope spécial
Je l'ai figé, mais sans doute serait-il intéressant de le rendre modifiable car il est utilisé conjointement avec la régularisation (mais pas seulement).
1) Il faudrait rajouter un deuxième mot clé après la régularisation
2) supprimer le fait qu'actuellement il s'agit d'un paramètre static, et le définir comme une variable analogue à la régularisation
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier loi_o1_o2_3D.hz_loi loi_o1_o2_3D.hz_loi ajouté
- Fichier loi_o1_o2.hz_loi loi_o1_o2.hz_loi ajouté
Un des problèmes vient bien des calculs initiaux petite déformation et en lien avec la phase. Et j'ai finalement les mêmes pb entre Orgéas 1 et Orgéas 2 pour une même situation donnée.
J'ai un mieux en mettant beaucoup d'itérations et dichotomie Newton contrainte plane :
nb_iteration_maxi_ 200
nb_dichotomie_maxi_ 10
ça permet de faire passer certains calculs mais ça peut être très long en début de simulation et sans garantie de succès. Avec un vrai maillage, ça restera problématique. J'ai un exemple de calcul relaxation dynamique fourni par Frank qui ne passe pas dès qu'il enclenche cette loi (quelque soit les stratégies : régularisation, loi des mélanges en def_duale_mises, beaucoup d'itérations Newton, etc...). soit ça plante, soit ça pédale dans la semoule (cas avec beaucoup d'itérations Newton).
A noter que je reviens sur ce que j'ai dit au message précédent. Je me suis trompé sur la sensibilité de cos3phi au facteur de régularisation. Le facteur de régularisation devrait avoir une influence visible sur le résultat, ce que je n'obtiens jamais en traction uniaxiale => même résultat que je mette fact_regul = 1.e-12, 1.e-8 ou 1.
Dans Herezh, on a : cos(3phi) = 3*sqrt(6)*J3/Qeps**3
en prenant en compte une régularisation, ça donne : cos(3phi) = 3sqrt(6)*J3/(Qeps + fact_regul)**3
NB : J3 n'est pas concerné par la régularisation.
si on regarde ce que ça donne "à la main" :
supposons un tenseur EPS de type "traction uniaxiale" égal à EPS11 = 1, EPS22 = EPS33 = 0.45 (Tij = 0 pour i différent de j) sans régularisation => cos(3phi) = 1 ; phi = 0
ça donne en valeur de cos(3phi) et angle phi en degrés :
- regularisation = 1.e-12 => cos(3phi) = 0.999999999997466 ; phi = 4.29977677777855e-05
- regularisation = 1.e-8 => cos(3phi) = 0.999999974660452 ; phi = 0.00429947880306878
- regularisation = 1. => cos(3phi) = 0.159315091125293 ; phi = 26.9442853639043
donc notamment, avec regularisation = 1., on se retrouve avec un angle de Lode se rapprochant d'un "cisaillement simple".
Pourtant, quand je fais une simulation de traction uniaxiale avec peu importe Orgéas 1 ou Orgéas 2, je n'ai strictement aucune variation de ma courbe résultat quelque soit la valeur de regularisation. Même une petite différence de cos3phi devrait se voir par réactualisation de ma courbe gnuplot. Et pourtant, je ne vois rien, ce qui veut dire que les valeurs dans le .maple sont strictement les mêmes et donc insensible à la régularisation.
Pour clarifier les lois, j'ai remis en pièce jointe un fichier avec juste les 2 lois : Orgéas 2 MAT_o2 et son équivalent Orgéas 1 MAT_o1. Ces 2 lois donnent le même résultat.
j'observe le même pb si je refais un calcul similaire mais sans contrainte plane (traction uniaxiale 3D sur un hexaedre). J'ai également joint la version 3D de ces lois.
Mis à jour par Julien Troufflard il y a plus de 2 ans
j'ai oublié une partie importante de mon message précédent :
pour revenir sur l'aspect que tu évoquais (paramètres qui permet de filtrer les petites valeurs : limite_inf_bIIb, etc...)
j'ai également vu ligne 44 du fichier Hyper3D.cc, la limite suivante :
double Hyper3D::limite_inf_Qeps = sqrt(2)*6.e-5 ;
utilisée notamment ligne 844 :
if ((inv_ret.Qeps >= limite_inf_Qeps)||(avec_regularisation))
mais on voit que toute utilisation de avec_regularisation_ dans le .info squizze ce test, quelque soit la valeur de fact_regularisation)
mais n'empêche, par défaut, la phase n'est pas calculée si Qeps est inférieur sqrt(2)*6.e-5, soit environ 8.5e-5
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier loi_o1_o2.hz_loi loi_o1_o2.hz_loi ajouté
j'ai fait une tentative pour voir en créant moi-même une régularisation selon def_duale_mises et une dépendance à Cos3phi_eps. Je l'ai fait en imbriquant 2 lois de mélanges. ci-joint le même fichier de lois que message précédent avec ajout de la loi MAT_o1_melange.
Pas très efficace comme concept mais je n'ai plus tellement d'alternatives maintenant.
malheureusement, la grandeur Cos3phi_eps n'est pas dispo aux pti.
Je n'ai plus trop d'idée pour répondre aux demandes de calcul dimensionnement de Frank. Seule la loi d'Orgéas pourrait le faire.
Est-ce que tu as regardé au sujet de la régularisation des lois Orgéas 1 et 2 ?
Mis à jour par Gérard Rio il y a plus de 2 ans
J'avoue que je suis un peu perdu sur tes demandes ?? qu'est-ce qu'il faudrait que je regarde concernant la régularisation ?
sinon concernant le cos3phi eps, normalement il est accessible au pti via les invariants de la loi hyperélastique ...mot clé "COS3PHI_EPS"
Mis à jour par Julien Troufflard il y a plus de 2 ans
oui désolé, j'ai besoin de cette loi et je vais un peu dans tous les sens pour trouver une solution ou une alternative. Et j'ai mal diagnostiqué l'influence du facteur de régularisation (que je croyais peu influente alors qu'en fait non).
Repartons sur une nouvelle base en regardant uniquement le répertoire en pièce jointe de ce message.
répertoire qui contient :
- un calcul de traction uniaxiale
- 2 lois de comportement : une orgéas 1 et une orgéas 2 (remarque : ces 2 lois donnent exactement le même résultat)
- fichier gnu pour tracer EPS11-SIG11
demande 1 :
est-ce normal que le facteur de régularisation n'ait aucune influence sur le calcul dans ces 2 lois de comportement ? on peut mettre 1e-12, 1., 10000., les résultats dans le .maple ne change pas d'un digit.
Pourtant, plus on augmente le facteur de régularisation, plus on se retrouve avec un angle de Lode de type cisaillement. Dans le script calcul_th_Lode.pl, il s'agit d'un calcul théorique du cos3phi tel que dans le fichier source Herezh Hyper3D.cc. J'ai mis un tenseur de déf de type traction uniaxiale (EPS11=1., EPS22 = EPS33 = - 0.45). La première variable ($regul) permet d'ajouter une régularisation de la même manière que Herezh et on voit bien l'énorme influence de ce facteur.
=> Mais Herezh, lui, ne semble pas affecté par la taille de cette valeur. Or, toute modification de cos3hpi par la régularisation devrait, même légèrement modifier les paramètres et donc forcément je devrais obtenir un peu de variation dans le résultat .maple.
demande 2 :
si malgré tout il s'agit d'un fonctionnement normal (que j'aimerais comprendre le cas échéant), pourquoi le calcul semble pédaler au départ avec la loi MAT_o1 (Orgéas 1) et non avec la loi MAT_o2 (Orgéas 2) ?
ps : si ces 2 lois ne peuvent pas tourner comme j'espère, j'aurai d'autres demandes pour faire des essais avec une loi de mélange
Mis à jour par Gérard Rio il y a plus de 2 ans
J'ai introduit les modifs suivantes:
- mise en place de la possibilité de définir les deux paramètres de limite inf:
limite_inf_Qeps et limite_inf_bIIb
cf. doc dans Herezh (il faut créer une nouvelle loi en interactif pour avoir la doc)
- sortie dans le .BI à l'incrément 0 de la valeur des paramètres :
régularisation limite_inf_Qeps et limite_inf_bIIb
ce qui permet de vérifier qu'ils ont la bonne valeur
ceci pour les lois: Favier, Orgeas 1 et 2, hyperbulkgene et 3D
- modif des I/O sur fichier .BI et .info
ça fonctionne et je m'aperçois que ton facteur de regularisation n'est pas bien placé dans le .info et donc il n'est pas pris en compte ce qui explique sans doute pourquoi il n'a aucune influence il faut mettre le facteur de regularisation juste avant le mot cle sortie_post_ éventuel donc cela fait dans ton exemple:
MAT_o1 LOI_CONTRAINTES_PLANES
NEWTON_LOCAL avec_parametres_de_reglage_
nb_iteration_maxi_ 200
nb_dichotomie_maxi_ 10
tolerance_residu_ 1.e-6
tolerance_residu_rel_ 1.e-5
mini_hsurh0_ 0.1
maxi_hsurh0_ 10.
fin_parametres_reglage_Algo_Newton_- 3K Qs mu1 mu2 mu3 alpha1 alpha2 Qe
6000. 3.5 55. 1.5 0.1000000000E-05 0.03 0.3000000000E-01 999.0000000 \
avec_phase
nQs= -1. gammaQs= 0.142857142857143 \
nMu1= -1. gammaMu1= -0.0909090909090909 \
nMu2= -1. gammaMu2= 0.333333333333333 \
avec_regularisation_ 1000000.
fin_loi_contrainte_plane
dit moi ce que cela donne avec cette mise en données
Mis à jour par Julien Troufflard il y a plus de 2 ans
merci pour les 2 paramètres introduits.
Pour la régularisation, ça fonctionne maintenant pour la loi Orgéas 1.
Par contre, pas évident de savoir où mettre les continuations de lignes. L'écriture que tu as proposée ne fonctionne pas. (NB : je teste sur la version d'avant => 7.014)
C'est cette écriture qui fonctionne :
ISOHYPER3DORGEAS1
# 3K Qs mu1 mu2 mu3 alpha1 alpha2 Qe
6000. 3.5 55. 1.5 0.1000000000E-05 0.03 0.3000000000E-01 999.0000000 \
avec_phase \
nQs= -1. gammaQs= 0.142857142857143 \
nMu1= -1. gammaMu1= -0.0909090909090909 \
nMu2= -1. gammaMu2= 0.333333333333333
avec_regularisation_ 1.e-12
Je ne comprends pas la nécessité du symbole continuation après le mot-clé "avec_phase". Sachant que ce symbole n'est pas requis si on ne met pas "avec_regularisation_ 1.e-12".
aucune écriture ne fonctionne sauf celle précédente
Bon c'est super pour Orgéas 1. Je vais pouvoir tester cette loi dans des cas plus complexes. ça fait déjà une solution dans le cas d'une dépendance cos3phi linéaire.
Concernant Orgéas 2, je n'ai trouvé aucune écriture qui fonctionne. Est-ce que tu pourrais me préciser à quel emplacement Herezh le cherche ? Et il reste ensuite à savoir où mettre des symboles continuation de ligne.
je ne vais pas reporter ici toutes mes tentatives. Selon les cas, j'ai soit une erreur à la lecture du .info, soit un calcul qui se lance mais qui peine à converger.
Mis à jour par Gérard Rio il y a plus de 2 ans
essai avec la version suivante qui fonctionne pour moi (avec la nouvelle version, mais normalement cela devrait marcher avec la tienne ?
MAT_o2 LOI_CONTRAINTES_PLANES
NEWTON_LOCAL avec_parametres_de_reglage_
nb_iteration_maxi_ 200
nb_dichotomie_maxi_ 10
tolerance_residu_ 1.e-6
tolerance_residu_rel_ 1.e-5
mini_hsurh0_ 0.1
maxi_hsurh0_ 10.
fin_parametres_reglage_Algo_Newton_- 3K Qs mu1 mu2 mu3 alpha1 alpha2 Qe
6000. 4. 50. 2. 0.1000000000E-05 0.03 0.3000000000E-01 999.0000000 \
avec_regularisation_ 1000000. \
avec_phase
Q0s_phi= COURBEPOLYNOMIALE
debut_coef= 0.875 0.125 fin_coef
mu01_phi= COURBEPOLYNOMIALE
debut_coef= 1.1 -0.1 fin_coef
mu02_phi= COURBEPOLYNOMIALE
debut_coef= 0.75 0.25 fin_coef \
avec_regularisation_ 1000000.fin_parametres_avec_phase_fin_loi_contrainte_plane
Mis à jour par Gérard Rio il y a plus de 2 ans
non, j'ai répondu un peu trop vite !
l'écriture qui me convient est la suivante, mais il faut la nouvelle version: 7.015
je vais la mettre sur le serveur.
MAT_o2 LOI_CONTRAINTES_PLANES
NEWTON_LOCAL avec_parametres_de_reglage_
nb_iteration_maxi_ 200
nb_dichotomie_maxi_ 10
tolerance_residu_ 1.e-6
tolerance_residu_rel_ 1.e-5
mini_hsurh0_ 0.1
maxi_hsurh0_ 10.
fin_parametres_reglage_Algo_Newton_- 3K Qs mu1 mu2 mu3 alpha1 alpha2 Qe
6000. 4. 50. 2. 0.1000000000E-05 0.03 0.3000000000E-01 999.0000000 \
avec_regularisation_ 1000000. \
avec_phase
Q0s_phi= COURBEPOLYNOMIALE
debut_coef= 0.875 0.125 fin_coef
mu01_phi= COURBEPOLYNOMIALE
debut_coef= 1.1 -0.1 fin_coef
mu02_phi= COURBEPOLYNOMIALE
debut_coef= 0.75 0.25 fin_coef
fin_parametres_avec_phase_
avec_regularisation_ 1000000.fin_loi_contrainte_plane
Mis à jour par Julien Troufflard il y a plus de 2 ans
ok, je vais regarder.
Il faut que je vois l'implication des 2 autres paramètres que tu as ajouté dans cette nouvelle version.
J'ai constaté quelque chose que j'espère résoudre avec ces 2 nouveaux paramètres.
Avec la version 7.014, quand on enlève la régularisation et que l'on met un pas de temps initial de 0.01 pour éviter les pb, on obtient le même comportement entre les deux lois o1 et o2.
Par contre, si j'enclenche la régularisation sur o1 et que je mets un facteur insignifiant (1e-12, 1e-20, ...), j'obtiens environ 1 MPa de moins qu'avec la loi sans régularisation.
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier loi_o1_o2.hz_loi loi_o1_o2.hz_loi ajouté
- Fichier loi_o1_o2_3D.hz_loi loi_o1_o2_3D.hz_loi ajouté
- Fichier test_3D.CVisu test_3D.CVisu ajouté
- Fichier test_3D.info test_3D.info ajouté
après test de la version 7.015 avec les lois pièce jointe :
1) d'après doc interactive, a priori les 2 nouveaux paramètres concernent le cas sans régularisation. Après test sur calcul avec MAT_o1 en les mettant très petits pour les désactiver (1e-30), je n'ai pas d'effet sur mon résultat de calcul (j'obtiens toujours un résultat inférieur de 1 MPa à ce que je dois obtenir, cf message précédent)
2) j'ai ajouté 2 lois :
- MAT_o1_TU => cas sans dépendance phase en calculant les coefs MAT_o1 pour cos3phi=1 (traction uniaxiale, soit idem que les coefs de base de MAT_o2)
- MAT_o1_CS => cas sans dépendance phase en calculant les coefs MAT_o1 pour cos3phi=0 (cisaillement simple, soit les coefs de base de MAT_o1)
Après test, il apparait que la loi MAT_o1 donne un résultat équivalent à MAT_o1_CS. Par conséquent, j'en conclus que si j'enclenche la régularisation sur MAT_o1, Herezh ne tient plus compte de la dépendance à la phase. Et si je supprime la dépendance à la phase sur MAT_o1, il tient compte de la dépendance à la phase
3) j'ai testé un peu la loi MAT_o2 (Orgéas 2). J'ai bien une influence de la régularisation, mais pas de convergence pour certaines valeurs de régularisation. Par exemple, si je mets 1e-4, il ne converge pas. J'ai peur d'obtenir le même problème avec MAT_o1 après débuggage de la dépendance à la phase en présence d'une régularisation.
Quel est le cheminement qui conduit à une non convergence de la contrainte plane ?
4) j'ai joint également un cas 3D (test_3D.info, .CVisu et lois dans loi_o1_o2_3D.hz_loi). Mêmes lois dédiées à un calcul sur un hexaedre. J'ai essayé MAT_o1. J'obtiens le même résultat qu'avec MAT_o1 3D CP, donc un résultat sans dépendance à la phase.
Ce qui est intéressant avec ce test 3D, c'est qu'il met en évidence des pb de lecture du .info. Je n'arrive pas à obtenir une influence du coef de régularisation avec MAT_o1.
De plus, la loi MAT_o2 fait complètement bugger la lecture du .info à écriture égale avec le cas 3D CP.
Mis à jour par Gérard Rio il y a plus de 2 ans
" j'obtiens toujours un résultat inférieur de 1 MPa à ce que je dois obtenir, cf message précédent) "
- au début ou a la fin du calcul ?
- c'est peut-être du au déclenchement du calcul en différence fini qui n'est pas pareil avec ou sans régularisation : cf. le booleen "avec_regularisation" dans le fichier Hyper3D.cc
" Après test, il apparait que la loi MAT_o1 donne un résultat équivalent à MAT_o1_CS. Par conséquent, j'en conclus que si j'enclenche la régularisation sur MAT_o1, Herezh ne tient plus compte de la dépendance à la phase. Et si je supprime la dépendance à la phase sur MAT_o1, il tient compte de la dépendance à la phase "
là je ne comprends pas ?
" Par exemple, si je mets 1e-4, il ne converge pas "
oui, il faut par exemple une régularisation de 0.1 pour une convergence
En fait la régularisation est une technique qui est une alternative à la loi des mélanges. Avec les mélanges, on peut mieux gérer ce qui se passe pour une intensité du déviateur faible mais il faut plus cogiter sur la transition.
Ceci étant, je ne sais pas si la notion de phase est pertinente vis-à-vis de l'expérience pour les faibles valeurs de l'intensité du déviateur des déformations ?? et même si elle est pertinente est-ce c'est un pb de faire une approximation au démarrage du chargement...
Comme on est en hyperélasticité il n'y a pas de mémorisation, c'est simplement un trajet de chargement pour la loi qui ne suivra pas exactement le modèle théorique asymptotique à l'origine.
Par contre c'est mieux que la loi cp et cp2 soit suffisamment robuste.
" De plus, la loi MAT_o2 fait complètement bugger la lecture du .info à écriture égale avec le cas 3D CP. "
- que ce soit avec la loi 1 ou 2, je n'ai pas de pb de lecture ?? avec ton test
- que faut-il faire pour voir le pb de lecture ?
Mis à jour par Julien Troufflard il y a plus de 2 ans
petit commentaire général avant de répondre à tes 4 points en gras :
L'idée générale de ce test est de comparer 2 lois qui sont sensées donner le même résultat. Compte-tenu de la forme des fonctions, la loi Orgéas 1 et Orgéas 2 proposées n'ont pas les mêmes paramètres dans le fichier loi. Mais un calcul rapide des coefs montrerait facilement qu'en fait ces 2 lois ont des coefs identiques pour un même angle de Lode.
ce n'est pas évident de reproduire les divers bugs que je constate. Il faut tester les lois pour s'en rendre compte en variant le pas de temps, la régularisation, en switchant entre loi o1 et o2. Et je ne trouve aucune robustesse dans ces calculs pourtant très simples.
les pb de convergence se passent à faible pas de temps, mais une infime variation peut générer une non convergence ou non. La loi Orgéas 2 semble la moins propice à convergence, avec pourtant une loi de dépendance linéaire tout comme la version Orgéas 1.
ça veut dire que quand on lance un calcul avec une des lois, on obtient un résultat. Ce résultat, on peut l'afficher en lançant le fichier gnu joint avec le répertoire de test (affichage EPS11-SIG11). Ensuite, on change la loi, on lance le calcul, on regarde le changement sur la courbe. Normalement, il ne devrait y avoir aucun changement puisque ces lois sont identiques dans leur dépendance à Lode. Or, je constate des différences.
Ensuite, concernant la convergence, il est étrange que ces 2 lois ne suivent pas la même convergence, puisque leurs lois de dépendance sont équivalentes et très simples (linéaires).
Concernant la régularisation, le rôle de ce paramètre est d'éviter les pb en petite déf et devrait à peu près ne concerner que le premier pas de temps. Il n'est pas question de mettre une valeur trop grande sinon on modifie complètement le résultat (cf le script perl qui montre l'influence sur l'angle Lode). Dans l'idée, je m'attends à mettre 1.e-12, voire 1.e-10. Si on met par exemple 0.1, le comportement n'a rien à voir avec la loi d'orgine.
De plus, dans mon esprit, cette valeur ne devrait pas influencer la convergence d'une loi. Et ce n'est d'ailleurs pas son rôle. Ce qui nuit à la convergence par exemple, ce serait un flip-flop autour d'un seuil (typique d'une loi de mélange par exemple ou autre discontinuité comme une conditionnelle d'un point de vue informatique). Mais dans le cas d'une régularisation, aucune surprise à ce sujet. Tout est régulier. Le cos3phi est borné, donc sans surprise lui aussi. Par exemple, une loi régularisée de Maheo ne pose aucun problème, que ce soit la loi Maheo hyper d'origine ou toutes les versions faites moi-même via une loi hyper_externe_W.
Je ne pense pas qu'il y ait un souci de non convexité ou autre. Il y a peu de variation sur les paramètres avec les dépendances que j'ai mis dans le fichier loi. J'ai voulu tester une loi très simple avec peu de différence entre les 2 extrémités du domaine cos3phi. N'importe quelle combinaison de ces paramètres donnerait une loi de comportement sans phase qui convergerait très bien sur tout type de sollicitation (sur un élément unitaire certes, mais sans souci néanmoins).
L'histoire de ce ticket est un peu la suivante : au début, je pensais juste à une demande d'ajout d'un nouveau paramètre (dépendance sur alpha1).
Ensuite j'ai peu à peu pris conscience des grandes difficultés de convergence de cette loi et du côté aléatoire de cette non convergence. Et je trouve ça surprenant.
Et enfin, mes tests d'aujourd'hui me montrent que parfois Herezh lit mal les paramètres d'entrée (pouvant même complètement zapper la dépendance à Lode).
réponses aux points dans des messages à suivre.
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier difference_o1_o2_pb_phase.tar difference_o1_o2_pb_phase.tar ajouté
concernant les points 1) et 2) :
pour reproduire ce que j'ai vu, il faut
a) mettre un pas de temps ini de 0.01 (comme ça pas de non convergence au départ)
b) enclencher une régularisation à 1.e-12 dans les lois MAT_o1 et MAT_o2
c) lancer le calcul avec la loi MAT_o2
d) dans un autre terminal : afficher le résultat avec : gnuplot gnu
e) changer la loi dans le .info => choisir la loi MAT_o1
f) lancer le calcul
g) réactualiser l'affichage gnuplot
=> tu devrais constater un baisse générale de toute la courbe (ordre de grandeur 1 MPa au dernier point calculé)
pour aller plus loin sur ce test, ci-joint un répertoire où j'ai comparé :
MAT_o2 en contrainte plane (MAT o2 3D CP)
MAT_o1 en contrainte plane (MAT o1 3D CP) avec régularisation
MAT_o1 en 3D normal sur un hexaedre (MAT o1 3D)
MAT_o1_TU qui est la version sans phase de la loi avec les coefs que l'on aurait pour cos3phi=1 (traction uniaxiale)
MAT_o1_CS qui est la version sans phase de la loi avec les coefs que l'on aurait pour cos3phi=0 (cisaillement simple). C'est-à-dire strictement les coefficients de base de la loi MAT_o1
MAT_o1 en contrainte plane (MAT o1 3D CP sans regul) sans régularisation
ci-joint directement les .maple de ces 6 résultats et un fichier gnu pour les superposer.
=> on voit que la loi MAT_o2 3D CP donne un résultat identique à :
1) la loi sans phase MAT_o1_TU
2) la loi MAT_o1 sans régularisation
=> on voit que la loi MAT_o1 donne un autre résultat identique :
1) dans sa version 3D CP et 3D normal
2) à la loi MAT_o1_CS
=> donc la loi MAT_o1 ne tient pas compte de la phase si on enclenche la régularisation. On obtient la même chose que la loi sans phase MAT_o1_CS. Si on enlève la régularisation, la phase fonctionne normalement, on retombe sur la loi MAT_o1_TU.
La loi MAT_o1_TU est elle-même identique à la loi MAT_o2. Mais à ce stade, je ne sais pas si la phase fonctionne pour MAT_o2 (car tu pourras remarquer que les coefs de base de la loi MAT_o2 sont les mêmes que la loi MAT_o1_TU; donc si ça se trouve la phase ne marche pas non plus avec MAT_o2 si on enclenche la régularisation)
ps : un point positif tout de même => la loi Orgéas 1 fonctionne de la même manière entre 3D et 3D CP. donc pas de pb à ce sujet
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier exemple_regul.png exemple_regul.png ajouté
réponse au point 3) : sur la valeur de régularisation 1e-4
comme dit précédemment, on ne peut pas mettre une régularisation trop grande. une valeur 0.1 modifie le comportement de manière visible.
par exemple en pièce jointe : la loi MAT o1 avec regul 1e-12 et regul 0.1
outre la question de l'influence de la régul, une autre question est : pourquoi une loi converge avec un certain coef de régularisation et pas un autre ?
Par exemple, la loi MAT o1 n'a pas de problème de convergence quelque soit la régularisation. Mais ça rejoint le point 1) et 2) => Herezh ne tient tout simplement pas compte de la dépendance à la phase si on met une régul. Donc il faudra que je revienne sur ce point quand ce pb sera résolu.
Je suis d'accord avec ton commentaire qui conclut ce point => peu importe la phase au départ du moment que ça converge. Mais si jamais on introduit un seuil pour ne pas tenir compte de la phase en très petite déf, alors on va retomber sur des cas particuliers, des flip-flop, etc..
il faut laisser la régularisation jouer son rôle naturellement et la répercuter dans les opérateurs tangents partout où Qeps se retrouve au dénominateur.
Mis à jour par Julien Troufflard il y a plus de 2 ans
réponse au point 4) sur le bug de lecture sur MAT o2 :
ah oui tu as raison. Avec la nouvelle version 7.015, il n'y a plus ce bug de lecture avec les lois 3D normale (test_3D.info).
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier pb_3D_petite_def.tar pb_3D_petite_def.tar ajouté
- Fichier exemple_pb_methode_dfc.png exemple_pb_methode_dfc.png ajouté
Gérard,
j'ai peut-être une piste concernant la non convergence petite déf. On voit mieux le problème petite déf en restant en 3D normale. Je joins ici un répertoire de test sur un hexaedre.
Dans ce répertoire, j'ai un fichier qui contient 2 lois Orgéas 2 :
- loi MAT_o2 => idem que précédemment
- loi MAT_o2_idem_o1 => j'ai reproduit la loi Orgéas 1 MAT_o1 en prenant Orgéas 2 + dépendance via courbe 1D COURBE_EXPO_N
NB : peu importe le contenu de ces lois
Dans le fichier test_3D.info, j'ai mis un pas de temps ini très petit (1.e-5).
Dans le fichier loi, j'ai désactivé la régularisation et j'ai indiqué les 2 nouveaux paramètres : limite_inf_Qeps_ et limite_inf_bIIb_
Je leur ai affecté même valeur que dans le fichier source Hyper3D.cc ligne 44 et 45 :
double Hyper3D::limite_inf_Qeps = sqrt(2)*6.e-5 ; //001;
double Hyper3D::limite_inf_bIIb = 36.e-10; // limite en dessous de laquelles on fait une ope spécial
si je mets une régularisation, par exemple sur la loi MAT_o2_idem_o1, le calcul diverge. En désactivant la régularisation, le calcul converge. Dans ce cas, Herezh tient compte des 2 paramètres précédents dans divers if() du code. En réalité, par le test, je n'ai aucune influence de limite_inf_Qeps.
Par contre, mon calcul est influencé par la valeur de limite_inf_bIIb. Notamment, cette limite déclenche une méthode spéciale de calcul (a priori, Herezh passe dans le "else" ligne 316 de Hyper3D.cc). Je vois dans les commentaires : méthode par différence finie, calcul du potentiel sous la forme polaire au point actuel, etc..
A priori, cette méthode permet la convergence mais fournit un résultat erroné. Pour le voir, il faut :
1) lancer le calcul test_3D.info avec l'une des 2 lois (et régularisation désactivée)
2) lancer la visu gnuplot : gnuplot gnu
remarque : le résultat sera le même avec les 2 lois fournies
dans cette visu gnuplot, j'ai zoomé sur le début de la courbe (voir aperçu en pièce jointe : exemple_pb_methode_dfc.png).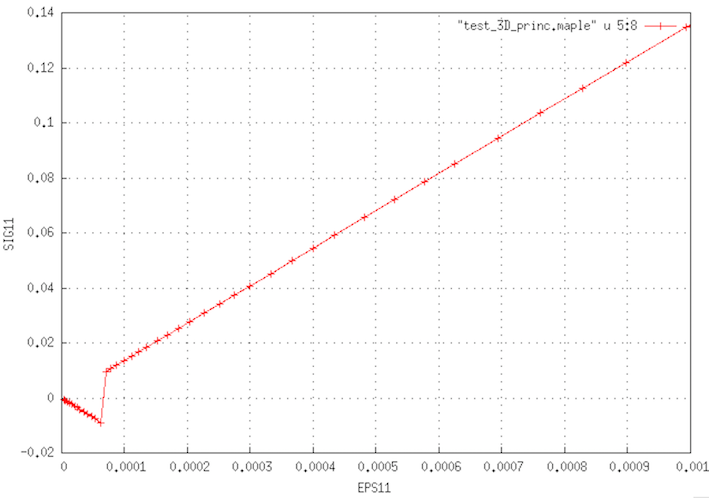
Une partie de la courbe est à SIG11 négative. Si on relance le calcul après modification de limite_inf_bIIb, on voit que la partie de la courbe où SIG11 est négative est directement en lien avec limite_inf_bIIb, donc avec la méthode par différence finie.
Ma conclusion actuelle serait que :
- la méthode par régularisation ne fonctionne pas en l'état (divergence du calcul)
- la méthode avec un seuil (if()) pourrait permettre la convergence malgré la discontinuité créé par ce seuil, mais ceci, sous réserve d'un correctif sur la méthode par différence finie. Elle conduit à une contrainte négative en traction uniaxiale, il y a clairement un problème.
je ne sais s'il faut regarder cette partie différence finie avant de regarder la régularisation.
Mis à jour par Gérard Rio il y a plus de 2 ans
- concernant le calcul en différence finie, je pense qu'effectivement il y a un pb et je crois voir où il est, mais je vais revoir les formules théoriques pour être sûr de ce que je fais.
- concernant la régularisation, j'ai aussi une idée: je crois qu'il manque des termes dans les dérivées. En fait ce qui est écrit est une approximation que je croyais suffisante, mais... peut-être que l'approximation n'est pas suffisante. Il faut que je regarde d'abord au niveau théorique.
donc ... à suivre
Mis à jour par Julien Troufflard il y a plus de 2 ans
super!
j'étais en train de errer sur le code source entre IsoHyper3DOrgeas2.cc et Hyper3D.cc
à suivre donc.
Mis à jour par Gérard Rio il y a plus de 2 ans
- % réalisé changé de 60 à 70
bon... j'ai modifié des choses sur le calcul en diff finie pour lequel j'avais une inversion de signe ... sur certains calculs mais pas tous !! et j'ai aussi mis des gardes fous au démarrage.
A priori, cela fonctionne: avec les deux lois en 3D avec ta sortie gnu j'obtiens maintenant une droite.
J'ai mis la nouvelle version sur le serveur: V 7.016
peux-tu regarder si c'est également ok pour toi ?
Je vais maintenant regarder du coté de la régularisation...
Mis à jour par Gérard Rio il y a plus de 2 ans
bon, en fait ce que je croyais être un pb avec la régularisation, c'était erroné.
Donc le pb à mon avis c'est que quand Qeps et trop petit on coupe les cheveux en quatre et la solution différence finie semble être la bonne solution.
Du coup, régularisation ou pas, je mets en oeuvre la diff finie pour Dabs(inv.bIIb) <= limite_inf_bIIb ceci dans le calcul des potentiels.
Par contre je laisse la possibilité d'utiliser la régularisation dans le calcul des invariants pour éviter les divisions par des nombres très petits pour des valeurs de Qeps très petit.
Bon... à tester
mais j'ai encore qq trucs à éclaircir
àsuivre
Mis à jour par Julien Troufflard il y a plus de 2 ans
merci pour la modif sur différence fini. ça fonctionne très bien. Tous mes tests simples fonctionnent comme prévu et c'est robuste à la valeur ini du pas de temps.
c'est ce que je constate en l'absence de régularisation.
la régularisation reste problématique. J'ai testé avec 1.e-12 (en conjonction avec limite_inf_Qeps_ et limite_inf_bIIb_) :
- les calculs divergent avec Orgéas 2. Est-ce bien dans cette version 7.016 que tu as modifié de manière à ce que Herezh passe en différence fini à petite déf même en présence de la régularisation ?
- la loi Orgéas 1 continue à zapper la dépendance à Lode. Mon hypothèse est que le symbole continuation de ligne après les paramètres de base fait que Herezh cherche le mot-clé avec_regularisation_ et donc passe complètement au-dessus de la partie "avec_phase". Je dis ça parce que la doc indique que le mot-clé avec_regularisation_ doit être placé à la suite des autres paramètres (ce que je comprends comme : "à la suite des paramètres de base")
- j'ai d'autres pb de lecture du .info avec Herezh, mais ça reste accessoire à l'heure actuelle (j'arrive à passer outre). pas trop envie de passer du temps là-dessus actuellement
je suis en train de tester un calcul de Frank avec cette nouvelle version. Malheureusement, il y a un souci mais c'est un calcul plus complexe et long. Je ne peux pas le diffuser ici.
J'aimerais bien reproduire ce bug avec un cas plus simple. Je te tiens au courant (sans doute un autre ticket ou par mail)
Mis à jour par Gérard Rio il y a plus de 2 ans
non, ce n'est pas dans la version 7.016 que j'ai intégré la régul, ce sera j'espère dans la nouvelle version.
Sinon, concernant la lecture des paramètres, tu peux regarder dans le .BI en rechercher le nom de la loi (au début) on y trouve tous les paramètres lus, ce qui permet de vérifier les valeurs utilisées pendant le calcul.
a suivre
Mis à jour par Gérard Rio il y a plus de 2 ans
- % réalisé changé de 70 à 80
suite:
- la modif de la régularisation est intégrée dans la version 7.017. Là on peut mettre un coef de regularisation très faible (il vaut mieux d'ailleurs) et dans tous les cas, pour une faible valeur de Qeps on passe en diff finie
- pour l'entrée des données, la syntaxe est (ex):
MAT_o2 ISOHYPER3DORGEAS2
# 3K Qs mu1 mu2 mu3 alpha1 alpha2 Qe
6000. 4. 50. 2. 0.1000000000E-05 0.03 0.3000000000E-01 999.0000000 \
avec_phase
Q0s_phi= COURBEPOLYNOMIALE
debut_coef= 0.875 0.125 fin_coef
mu01_phi= COURBEPOLYNOMIALE
debut_coef= 1.1 -0.1 fin_coef
mu02_phi= COURBEPOLYNOMIALE
debut_coef= 0.75 0.25 fin_coef
fin_parametres_avec_phase_
limite_inf_Qeps_ 0.0000848528 limite_inf_bIIb_ 3.6e-9 avec_regularisation_ 1.e-12
Mis à jour par Gérard Rio il y a plus de 2 ans
je viens de mettre à jour le dépôt git d'Herezh++ :
https://gitcdr.univ-ubs.fr/rio/Herezh_dev
tu peux regarder les modifs en:
1) en choisissant la branche 7.017
2) en cliquant sur sur le numéro de révision (à coté de "Gérard Rio")
il y a affichage de toutes les modifs avec 2 colonnes: à gauche la version originale, à droite la nouvelle version (sur le navigateur)
3) ensuite tu peux récupérer la nouvelle version avec git
remarque: j'ai utiliser la nouvelle version de codeblock via macport sur le mac et j'ai réussi à tout compiler et lancé l'exécution. Je mettrai les infos sur le roadmad dès que possible
Mis à jour par Julien Troufflard il y a plus de 2 ans
J'ai testé la loi MAT_o2 :
1) avec les param suivants : limite_inf_Qeps_ 5.e-9 limite_inf_bIIb_ 5.e-9 avec_regularisation_ 1.e-12
=> convergence et résultats ok
2) et ensuite (pour désactiver la partie différence fini) avec les param : limite_inf_Qeps_ 1.e-30 limite_inf_bIIb_ 1.e-30
en conjonction avec : avec_regularisation_ 1.e-12, 1.e-10, 1.e-8, 1.e-6, 1.e-4 et 0.1
=> pas de convergence quelque soit la valeur de la régularisation
donc au final, actuellement c'est la méthode de différence finie qui permet la convergence.
Je continue sur le cas de calcul de Frank. J'espère mettre en place un cas plus léger aujourd'hui.
Peut-être hors sujet dans ce ticket, mais juste pour que tu commences à envisager le pb, voici le genre de message d'erreur que j'ai actuellement (contrainte plane et contrainte plane double) :
exemple 1 :
LoiContraintesPlanesDouble::Calcul_et_Limitation2_h_b(..
**erreur: la deformation eps'_I 0.51387581) est superieur a 0.5, on ne peut pas s'en servir pour mettre a jour la variation de volume
**>> non convergence sur l'algo de la resolution de (sigma.V_2=0, sigma.V_3=0),
mail: 1, ele= 29, pti=1 , nb_incr_total=11, nb_iter_total=297, val obtenues:
eps_P(2,2)= -1.0492879, eps_P(3,3)= -0.82795204, eps_P(1,2)= -0.89475882
precedentes: 0, 0, 0
exemple 2 :
*** pb dans le calcul de la nouvelle epaisseur: le coef de compressibilite moyen = 2.665736e+11 est par rapport a delta la trace de sigma = 4.3907193e+240 10 fois inferieur !! ce n'est pas normal a priori on continue sans changer l'epaisseur ...
QuadraMemb::CalEpaisseurMoyenne_et_vol_pti(...)
Mis à jour par Gérard Rio il y a plus de 2 ans
- % réalisé changé de 80 à 90
oui, il faut utiliser la méthode des différences finies donc adapter les paramètres de contrôle.
En fait, maintenant les 3 paramètres contrôles des points différents, la régularisation intervient uniquement sur les 1/0 dans le calcul des invariants primaires, le bIIb limite inf intervient sur le déclenchement et la conduite (via le delta) du calcul en différence finie et le Qeps mini intervient sur le calcul de la phase et de ses dérivées.
Donc il faut utiliser les 3 ou... les 2 sans régul ?? là je ne sais pas ... à voir avec les tests
car en différence finie on considère que la phase est nulle.
pour le message d'erreur, on a une def > 0.5 avec almansi ! donc effectivement c'est une divergence
Pour avoir plus d'info précise, tu peux mettre un niveau de commentaire plus grand dans les algo de Newton et tu verras les différentes itérations... peut-être que cela permettra d'y voir plus clair ?
J'ai mis à jour la doc pdf et aussi celle dans le code (cf. git) par contre ce ne sera disponible dans l'exécutable que dans les versions à venir.
Peux-tu regarder sur le pdf pour voir si c'est suffisamment explicatif ?
Mis à jour par Julien Troufflard il y a plus de 2 ans
J'ai mis à jour la doc pdf et aussi celle dans le code (cf. git) par contre ce ne sera disponible dans l'exécutable que dans les versions à venir.
Peux-tu regarder sur le pdf pour voir si c'est suffisamment explicatif ?
oui pour ma part
sur la forme, j'ai un léger doute sur l'utilisation de la tournure '+=' qui est un symbole informatique. Mais plus concrètement, Latex a toujours eu du mal à faire un symbole + de la bonne taille (souvent trop gros) et le fait d'insérer "+=" dans un environnement "math" via $+=$ provoque un espacement entre le + et le = qui gène la compréhension. En l'occurrence, j'ai eu un peu de mal à comprendre la formule :
<pre><code class="xml">
si V < c alors V+ = c
</code></pre>
au premier coup d'oeil, j'ai cru que le + était collé au V avant de comprendre qu'il s'agissait de l'opérateur +=
bref : je dis pas qu'il faut modifier et publier une nouvelle révision de la doc maintenant.
ça serait moi, je modifierais maintenant dans le latex par des tournures du style V = V + c, histoire que cette modif soit incluse dans une prochaine réactualisation officielle de la doc.Mis à jour par Julien Troufflard il y a plus de 2 ans
la mise en forme de mon message précédent a complètement vrillé.
je réécris mon message en réponse à ta phrase :
"""
J'ai mis à jour la doc pdf et aussi celle dans le code (cf. git) par contre ce ne sera disponible dans l'exécutable que dans les versions à venir.
Peux-tu regarder sur le pdf pour voir si c'est suffisamment explicatif ?
"""
sur la forme, j'ai un léger doute sur l'utilisation de la tournure '+=' qui est un symbole informatique. Mais plus concrètement, Latex a toujours eu du mal à faire un symbole + de la bonne taille (souvent trop gros) et le fait d'insérer "+=" dans un environnement "math" via $+=$ provoque un espacement entre le + et le = qui gène la compréhension. En l'occurrence, j'ai eu un peu de mal à comprendre la formule :
si V < c alors V+ = c
au premier coup d'oeil, j'ai cru que le + était collé au V avant de comprendre qu'il s'agissait de l'opérateur +=
bref : je dis pas qu'il faut modifier et publier une nouvelle révision de la doc maintenant.
ça serait moi, je modifierais maintenant dans le latex par des tournures du style V = V + c, histoire que cette modif soit incluse dans une prochaine réactualisation officielle de la doc.
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier limite_inf_bIIb_5e-9.png limite_inf_bIIb_5e-9.png ajouté
- Fichier limite_inf_bIIb_5e-8.png limite_inf_bIIb_5e-8.png ajouté
- Fichier exemple_erreur_sans_pb_convergence.png exemple_erreur_sans_pb_convergence.png ajouté
Gérard,
pour info, une bonne nouvelle => j'ai des calculs qui convergent dans un cas de type bulge test et coussin carré.
à noter cependant des pb possibles en petite déf. Par exemple, ci-dessous, si je simule sur un élément une traction biaxiale avec un pas de temps ini de 1.e-5 et une limite_inf_bIIb_ égal à 5.e-9, j'obtiens une convergence mais ce comportement erroné avec la loi MAT_o2 :
si je passe limite_inf_bIIb_ à 5.e-8, le problème disparait :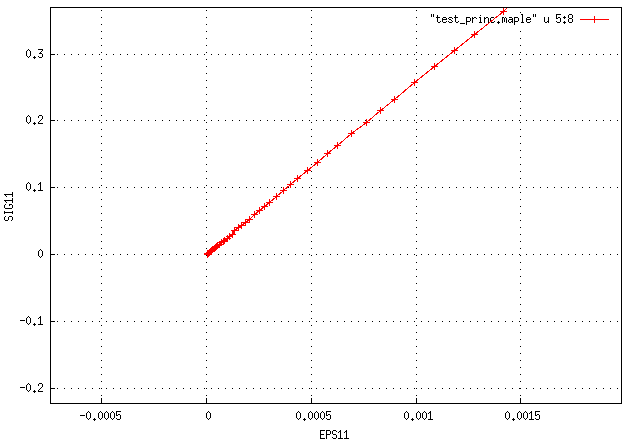
mais pour une autre loi orgéas 2 (paramètres qui n'ont rien à voir avec les lois de ce ticket), j'ai été obligé de passer limite_inf_bIIb_ à 1.e-6 pour régler le problème.
Ceci pose question. Ce n'est pas que un pb de convergence et d'opérateur tangent. Il y a également un impact sur la valeur de contrainte obtenue, ce qui est très problématique (ça pourrait signifier une erreur de calcul de la loi de comportement en elle-même).
De mémoire, je n'ai d'ailleurs pas forcément d'affichage d'erreur dans le terminal pour non-convergence. La loi convergerait correctement en contrainte plane mais donne une valeur de contrainte erronée.
voici un cas dont je peux fournir la mise en données par mail. J'ai un limite_inf_bIIb_ de 1.e-7, aucun affichage d'erreur sur la convergence et une erreur de contrainte :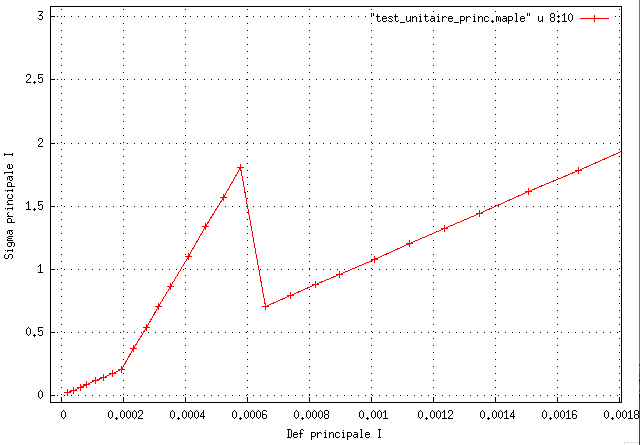
le pb disparait avec limite_inf_bIIb_ de 1.e-6
petite demande de confirmation au passage :
dans le cas d'une loi contrainte plane, la phase que reçoit la loi de comportement est bien le COS3PHI_EPS (c'est-à-dire la phase de la loi 3D) et non Cos3phi_eps qui est la phase pour une cinématique 2D ?
si je regarde le comportement, on dirait bien qu'il reçoit la valeur correcte qui est COS3PHI_EPS, mais je veux en être bien sûr. Parce que le Cos3phi_eps en 2D n'a rien à voir avec la réalité. Par exemple, au centre d'un bulge, j'obtiens un COS3PHI_EPS = -1 comme prévu mais un Cos3phi_eps = 1.73 qui n'a aucun sens.
Mis à jour par Gérard Rio il y a plus de 2 ans
concernant la phase, tout est calculé dans Hyper3D (cf. Hyper3D.cc) à partir de la déformation et de la métrique.
en contrainte plane double, il faut regarder: LoiContraintesPlanesDouble.cc et LoiContraintesPlanesDouble_2.cc
en particulier:LoiContraintesPlanesDouble::Mat_tangente_constitutif et LoiContraintesPlanesDouble::Residu_constitutif ou LoiContraintesPlanesDouble::Residu_constitutif_3D( et LoiContraintesPlanesDouble::Mat_tangente_constitutif_3D
c'est là que l'on fait appel à la loi 3D avec constitution de la déformation 3D
Mis à jour par Gérard Rio il y a plus de 2 ans
Je pense qu'il y a une interaction entre les différents paramètres.
-étape 1) on a des composantes de la def qui sont très petits. Là il y a un test dans le calcul final de la contrainte cf. HyperD.cc ligne 854:
double norm_i_epsBH = epsBH.MaxiComposante(); // norme infinie de la déformation
if ((norm_i_epsBH < ConstMath::petit)&&(!avec_regularisation))si le maxi de la composante < 1.e-10 et sans régul : calcul sans phase
- étape 2) on dépasse ConstMath::petit, du coup on appelle le calcul :
Hyper3D::PotentielPhase_et_var(...
Mais dans ce calcul il y a le test:
if (Dabs(inv.bIIb) > limite_inf_bIIb)Donc on peut imaginer: 2 sous étapes:
2.1 : Dabs(inv.bIIb) < ou = à limite_inf_bIIb : on fait de la différence finie :
2.2 : on est sup : on fait un calcul normal qui correspond peut-être dans ton cas à la première étape
Dans la partie 2.1: je ne calcule pas les dérivées suivant la phase, par contre j'utilise la phase pour le calcul du potentiel ce qui est peut-être problématique car sans régularisation, on peut avoir des angles de phase grands ou petit du à la division par 0, cf:
Hyper3D::Invariant0QepsCosphi Hyper3D::Invariant0Specif(const Invariant & inv)
inv_ret.Qeps = sqrt(2. * inv.bIIb);
double inv_ret_Qeps = inv_ret.Qeps; // init pour être éventuellement modifié
// ensuite avec la régularisation
if (avec_regularisation)
{inv_ret_Qeps += fact_regularisation;}
double unsurQeps = 1./inv_ret_Qeps; // pour simplifier
// --- angle de phase
double unsurQeps3 = unsurQeps * unsurQeps * unsurQeps;
double troisracine6 = 3. * sqrt(6.);
inv_ret.cos3phi = troisracine6 * inv.bIIIb * unsurQeps3;
if (inv_ret.cos3phi > 1.) inv_ret.cos3phi=1.;
if (inv_ret.cos3phi < -1.) inv_ret.cos3phi=-1.;
du coup on est peut-être bloqué sur un cos3phi de 1 ou -1 tant que l'on est en diff finie
puis arrive la phase 2.2
- as-tu utiliser la régularisation ?
si ce n'est pas le cas, peux-tu essayer ce qui permettra de passer par un autre chemin dans l'étape 1 et 2.1
. je me demande s'il ne faudrait pas tout simplement calculer le potentiel sans phase en 2.1 ce qui me semble à la réflexion, plus cohérent compte tenu de la succesion de tests actuels ?
. ceci étant avant de changer j'aimerais avoir ton retour avec la régul et peut-être avec tes tests par mail
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier Qeps_1e-9_bIIb_1e-9_regul_1e-4.png Qeps_1e-9_bIIb_1e-9_regul_1e-4.png ajouté
- Fichier Qeps_1e-4_bIIb_1e-9_regul_NON.png Qeps_1e-4_bIIb_1e-9_regul_NON.png ajouté
- Fichier Qeps_1e-4_bIIb_1e-4_regul_NON.png Qeps_1e-4_bIIb_1e-4_regul_NON.png ajouté
- Fichier Qeps_1e-4_bIIb_1e-9_regul_1e-10.png Qeps_1e-4_bIIb_1e-9_regul_1e-10.png ajouté
- Fichier TU_Qeps_1e-4_bIIb_1e-4_regul_NON.png TU_Qeps_1e-4_bIIb_1e-4_regul_NON.png ajouté
- Fichier TU_Qeps_1e-4_bIIb_1e-3_regul_NON.png TU_Qeps_1e-4_bIIb_1e-3_regul_NON.png ajouté
- Fichier Qeps_1e-4_bIIb_1e-9_regul_1e-6.png Qeps_1e-4_bIIb_1e-9_regul_1e-6.png ajouté
- Fichier Qeps_1e-4_bIIb_1e-5_regul_1e-6.png Qeps_1e-4_bIIb_1e-5_regul_1e-6.png ajouté
avant de montrer les tests, je voulais juste dire que je suis globalement d'accord avec une désactivation de la phase en petite déformation. Mais le fait est que dans le cas différence fini, le comportement calculé actuellement (donc avec la phase) est pas mal. Pas mal au sens où il y a une petite rupture de la courbe comportement au passage de limite_inf_bIIb_ entre la méthode différence fini et la méthode normale. Cette rupture est très légère, ce qui montre le bon calcul différence fini. Et donc question à vérifier :
que deviendra cette petite rupture si le comportement différence fini ne prend plus en compte la phase dans le cas d'une loi avec des paramètres qui évoluent beaucoup avec la phase ?
voici les tests que j'ai fait en nommant les fichiers résultat ainsi : Qeps_[valeur]_bIIb_[valeur]_regul_[valeur].png
avec la correspondante suivante sur les paramètres :
Qeps => limite_inf_Qeps_
bIIb => limite_inf_bIIb_
regul => avec_regularisation_
NB : une valeur "NON" signifie pas de paramètre indiqué dans le .info
à chaque fois il s'agit d'une traction équi-biaxiale (UX = 0.4 ; UY = 0.4)
je suis tombé sur un premier cas "rigolo" en mettant :
Qeps = 1.e-4 ou 1.e-9
bIIb = 1.-9
regul = 1.e-4
=> la contrainte est négative au départ, puis excessivement positive avec un pic avant de reprendre un comportement normal. L'allure est identique avec Qeps 1e-4 ou 1e-9, ce paramètre change juste légèrement les valeurs au pic avant reprise normale du comportement
même test avec une régul beaucoup moins forte. J'ai mis une valeur qui pourrait être considérée comme raisonnable : régul = 1e-10
=> pas de contrainte négative au départ, toujours un pic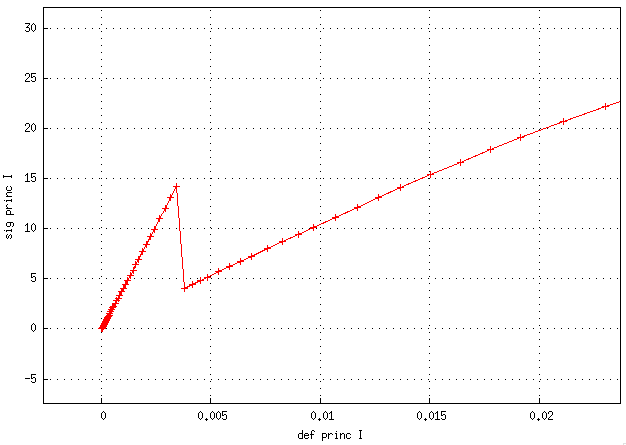
même test sans regul => pas de contrainte négative au départ, toujours un pic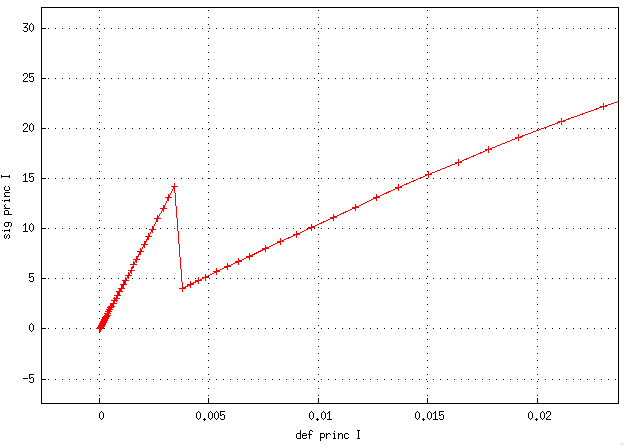
même test sans regul et bIIb = 1e-4 => comportement ok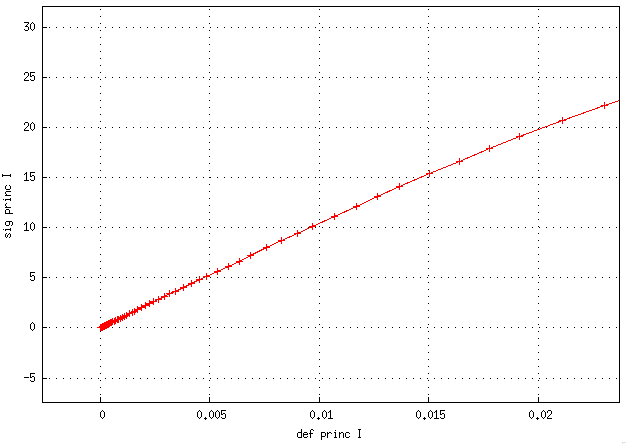
pour info, le même test sans regul et bIIb = 1e-3 donne également un comportement ok mais si je passe traction uniaxiale au lieu de biaxial, j'observe un impact sur le comportement. Si je mets aucune régul et un bIIb de 1e-4, j'obtiens le bon comportement suivant (similaire bIIb 1e-6 et moins) :
si je mets bIIb 1e-3, on commence à voir un écart avec cassure visible "méthode différence fini / méthode normale" :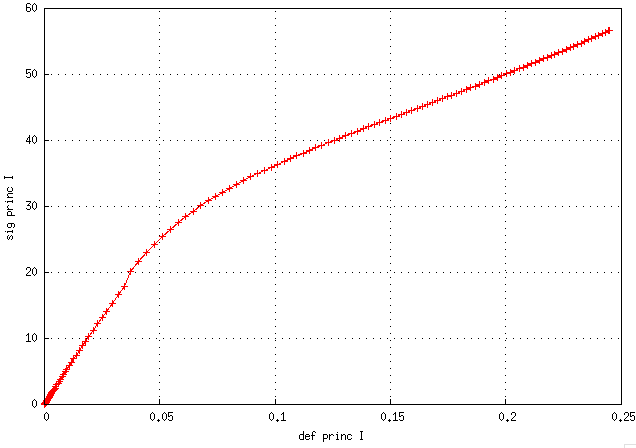
et pour finir, retour à la traction biaxiale avec deux autres exemples de résultats :
- Qeps = 1.e-4 ; bIIb = 1.e-9 ; regul = 1.e-6
=> une contrainte positive à la toute origine du graphe, suivi d'un passage en négatif, puis un gros pic avant reprise du comportement normal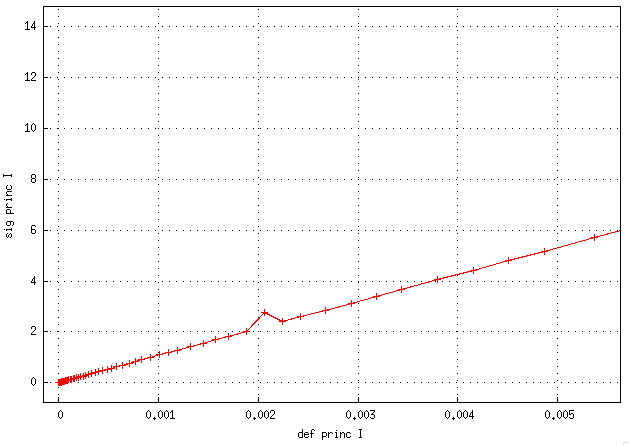
- Qeps = 1.e-4 ; bIIb = 1.e-5 ; regul = 1.e-6
=> comportement quasi normal avec juste un petit décroché vers 0.002 de déformation
Mis à jour par Julien Troufflard il y a plus de 2 ans
oups, attention, j'ai inversé les 2 derniers graphes
Mis à jour par Gérard Rio il y a plus de 2 ans
donc:
- a priori si on veut utiliser la régularisation, il faut choisir une très faible valeur 1.e-10 par exemple sinon on a quelque chose comme une inversion de phase à l'origine. Mais comme au tout début il n'y a pas de phase je trouve cela bizarre. a moins qu'il n'y a pas (ou pas visible) la phase 1) dont je parlais. Dans ce cas on est directement en diff fini et une trop grande valeur du facteur de régularisation peut introduire des choses vraiment pas normal au niveau du calcul de la phase.
tu pourrais mettre un niveau d'affichage à 8 pour la loi 3D pour voir (utiliser la version non fast): cf. void HyperD::Calcul_dsigma_deps (
- si on a de la regul, on a pas la phase 1) dont je parlais, on passe passe potentiellement directement en diff finie et là c'est limite_inf_bIIb qui décide finalement si on utilise la diff finie
- du coup compte tenu de tes remarques, je laisse en l'état avec diff finie utilisant le potentiel avec phase, mais pas de dérivées / à la phase:
J'aurai tendance à garder par défaut: une régul de 1.e-10, un limite_inf_bIIb de 1.e-4 qui est équivalent à un cisaillement de l'ordre de 1.e-2 MPa (ou encore 0.1 bar) ce qui est petit
et mettre le Q_eps lim en cohérence (ce serait en fait de l'ordre de sqrt(2.)*1.e-2: cf. sqrt(2*limite_inf_bIIb)
ce qui n'est pas vraiment ce qui est implanté !
,limite_inf_Qeps(sqrt(2)*6.e-5),limite_inf_bIIb(36.e-10), et pas de régul !
a voir ...