Evolution #386
ouvertLoi hypoélastique (log) en comportement sécant
Description
Bonjour Gérard,
est-ce qu'il y a un moyen de faire une loi élastique non linéaire similaire à la loi HYPOELAS mais en comportement sécant ?
Et si non, que penserais-tu de l'introduire dans Herezh ? J'imagine une sorte de copier/coller de la loi HYPOELAS, qui utiliserait le tenseur de déf log cumulé pour pouvoir faire sigma = C:epsilon et avec C égal au tenseur de rigidité sécant (qui pourra dépendre de fonctions nD via un Kc_s et mu_s, "_s" signifiant "sécant"). Le tenseur de déf cumulé est sans doute déjà dispo car il existe la grandeur DEF_ASSO_LOI.
Mon but est d'avoir une loi d'élasticité non linéaire assez libre sur sa forme grâce aux fonctions nD et qui dépend beaucoup moins du trajet de déformation que l'actuelle HYPOELAS. Il resterait juste l'erreur d'intégration de D propre à la déf log cumulée.
En vrai je ne sais pas si cette approche sécante sera radicalement différente de l'approche tangente. bonne idée ou fausse bonne idée ?
Ceci dit, je pourrais tester en python avant de se lancer dans les travaux Herezh (travaux que je réaliserai si l'idée te parait bonne)
a+
Fichiers
Mis à jour par Gérard Rio il y a 6 mois
- Fichier clipboard-202509020944-vj5uu.png clipboard-202509020944-vj5uu.png ajouté
- Fichier clipboard-202509020945-tsiwj.png clipboard-202509020945-tsiwj.png ajouté
- Statut changé de Nouveau à En cours
Bonjour Julien,
j'ai peut-être déjà mis en place une réponse à ta sollicitation.
Je suis en train de travailler sur la mesure de def log et log cumulé. Soit dit en passant le log cumulé peut-être très différent de la mesure log exacte quand les def sont très importante, mais sinon pour des def modérés (?) disons < à 0.5, c'est en générale très proche de la mesure log (si on choisit un pas de temps pas trop grand).
Je me rappelais que tu avais des pb de non conformité de la mesure log pour certains calculs donc j'ai passé pas mal de temps à regarder et j'ai réparé 2 bugs.
Du coup avec le comportement élastique + mesure log j'obtiens des résultats assez étonnants.
Par exemple je prends une barre de 100x10x10 mm maillé avec 10 éléments quadratiques complets en description et en intégration, et j'effectue une torsion = mvt de rotation imposée aux noeuds d'une extrémité.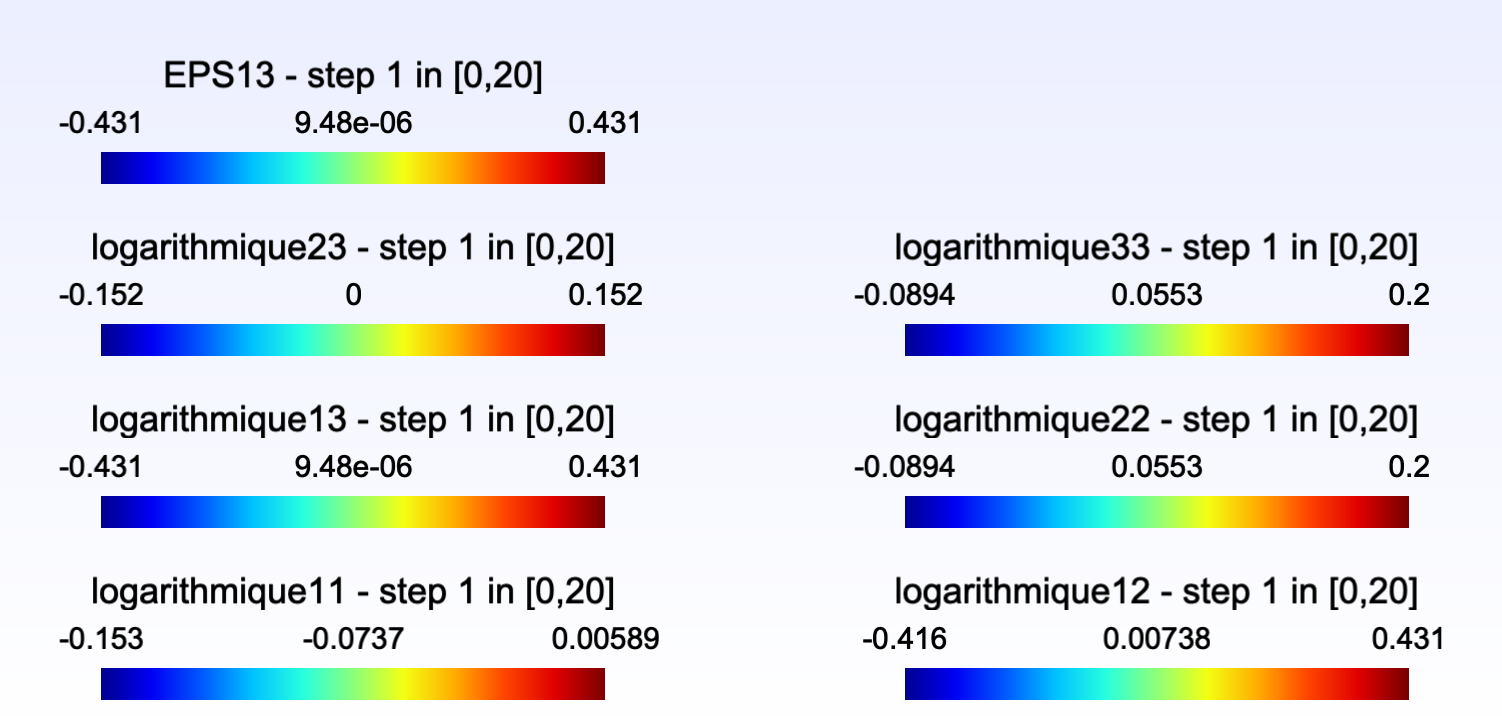
La convergence avec la mesure d'Almansi est limité (quelque chose dans les alentours de 600° ? ) contrairement à la mesure log qui ne pose aucun pb jusqu'à par exemple 720°
même vitesse de convergence quelque soit l'angle de torsion !! alors que je m'attendais à une dégradation de la convergence à mesure de la torsion comme ces le cas avec Almensi.
J'ai aussi comparé avec une loi hypo sur les tests qu'avaient utilisé Vincent Mora et j'obtiens exactement les mêmes résultats que lui.
Donc pour l'instant j'ai l'impression que la mesure log à l'air correct et en plus que l'opérateur tangent (donc testé avec la loi de Hooke) à l'air de fonctionner.
C'était pas gagné car les calculs sont plutôt compliqués !
Donc pour revenir à ta question, je pense que tu pourrais essayer d'utiliser la loi de Hooke avec la mesure log implantée:
- ça correspond par définition à l'utilisation d'un module sécant
- tu peux piloter les paramètres de la loi avec des fct nD
qu'en penses-tu ?
si c'est ok, je vais mettre à jour sur le serveur git
Mis à jour par Julien Troufflard il y a 6 mois
Et bien oui, cette loi pourrait correspondre à ce que je cherche. Le résultat est très joli en tout cas.
il faudrait que je teste.
Mis à jour par Gérard Rio il y a 6 mois
- Fichier cisaill_simple.CVisu cisaill_simple.CVisu ajouté
- Fichier cisaill_simple.info cisaill_simple.info ajouté
C'est ok avec la version 7.055
Pour info voici les fichiers que j'ai utilisé pour mes tests:
Mis à jour par Gérard Rio il y a 6 mois
- Fichier cube_trac_1puis2.info cube_trac_1puis2.info ajouté
- Fichier cube_trac_1puis2.CVisu cube_trac_1puis2.CVisu ajouté
- Fichier cycle_rotationnel.info cycle_rotationnel.info ajouté
- Fichier cycle_rotationnel.CVisu cycle_rotationnel.CVisu ajouté
- Fichier torsion.info torsion.info ajouté
- Fichier torsion.CVisu torsion.CVisu ajouté
- Fichier barre_qc_10x1x1.her barre_qc_10x1x1.her ajouté
- Fichier cube_1.her cube_1.her ajouté
- Fichier cube_1x1x1.her cube_1x1x1.her ajouté
Mis à jour par Gérard Rio il y a 6 mois
- % réalisé changé de 0 à 20
pour l'instant l'opérateur tangent dsig/deps en log n'est pas implanté. En fait je dois développer de manière théorique les dérivées de la métrique par rapport à la def log...ça promet !
mais cela veut dire que pour l'instant la loi de Hooke avec log est utilisable telle quelle mais pas avec une loi cp ou cp2 et donc pas avec un critère plis.
Donc j'ai encore du boulot !mais ça avance !
Mis à jour par Julien Troufflard il y a 6 mois
je peux déjà tester avec un élément hexa et comparer à une loi hypo 3D. Le vrai point qui m'intéresse est de voir comment elle se comporte dans une loi de mélange. J'ai actuellement des soucis avec une loi de mélange de lois hypo. Ce n'est pas un bug, mais une conséquence normale. Avec 2 lois pas de pb, mais le souci intervient quand on veut faire un mélange de 3 lois incrémentales ou plus. Et je pense qu'une loi non incrémentale est la solution (ça permet de replacer dans une situation similaire à des lois hyperélastiques).
Mis à jour par Gérard Rio il y a 6 mois
est-ce que tu peux préciser ton soucis avec la loi des mélanges avec + de 2 lois incrémentales... voir mettre un exemple,
Mis à jour par Julien Troufflard il y a 6 mois
ok pour expliquer la loi mélange dans un prochain message.
Avant toute chose, je voudrais juste dire que j'ai testé la loi ISOELAS en déf. log avec des fonctions nD. Pas de pb particulier sur le fonctionnement informatiquement parlant.
et je voudrais énoncer 2 problématiques en lien avec cette loi :
1) Je n'ai pas testé le vrai cas qui avait retenu mon attention en 2016 : compression uniaxiale suivie de cisaillement simple (en faisant un blocage_relatif_). Dans ce cas, il me semble (de mémoire) qu'il y avait un souci car lors de la compression uniaxiale, les 2 directions transverses ont la même déformation. Il me semble que la présence de 2 valeurs propres égales était l'une des situations à problème si on veut enchainer derrière un autre chargement. Je ne saurais plus expliquer ce qu'il se passait. A suivre sur ce point quand j'aurais testé.
2) Autre point que j'ai à résoudre et sur ce point j'aimerais bien en discuter ailleurs que sur redmine (trop long) : ma loi ISOELAS log tourne informatiquement, mais mécaniquement j'ai un défaut conceptuel. Je n'obtiens pas la même chose qu'un équivalent HYPOELAS. Est-ce que je pourrais te soumettre un document qui explique comment je paramètre (fonctions nD) mes 2 lois, sachant que je veux que ces 2 lois donnent le même résultat sur un trajet monotone.
et ensuite en discuter par visio (ou sur Lorient si besoin d'un tableau)
Mis à jour par Julien Troufflard il y a 6 mois
- Fichier exemple_trajet_complexe.png exemple_trajet_complexe.png ajouté
Concernant la loi de mélange :
J'ai un certain paramètre de mélange => typiquement l'angle de Lode ou quelque chose de même nature (un indicateur du mode de sollicitation à l'état actuel, basé sur le tenseur EPS actuel quelque soit l'histoire méca).
je note :
TU = traction uniaxiale
TB = traction équibiaxiale
TP = traction plane
supposons que j'ai une loi HYPOELAS nommée "LOI_TU" identifiée sur un essai TU, une loi "LOI_TB" sur un essai TB et une loi "LOI_TP" sur un essai TP.
Chacune de ces lois reproduit fidèlement le comportement expérimental qui a été utilisé pour l'identifier dans le mode de sollicitation concerné. Et donne un résultat quelconque si on la sollicite autrement.
supposons un mélange à 2 lois par exemple : LOI_TU + LOI_TP
=> pas de problème dans ce cas. A chaque incrément, il va y avoir un incrément de contrainte LOI_TU et un incrément LOI_TP. Ils sont calculés depuis l'incrément de déformation DEPS qui évolue de la manière nécessaire pour converger. Chaque incrément de contrainte est ajouté à sa loi. Et le mélange va avoir lieu entre la loi LOI_TU et la loi LOI_TP.
J'insiste sur le fait que le mélange a lieu sur le tenseur total actuel, et non pas sur l'incrément de contrainte.
Maintenant si je prends un mélange à 3 lois. Je passe par un mélange imbriqué avec une fonction de mélange F_1 permettant de calculer un mélange entre une LOI_TU à une seconde loi de mélange. Cette seconde loi de mélange est régie par une fonction F_2 permettent de faire un mélange entre LOI_TP et LOI_TB.
schéma de principe :
(LOI_TU) 1 --- F_1 --- 0 (LOI_TP) 1 ---- F_2 ---- 0 (LOI_TB)
dans un contexte de lois HYPOELAS, il y a 2 conséquences :
1) il est nécessaire de calculer tout le temps les 3 lois, même si on est par exemple uniquement dans le domaine F_1 (pas de mot-clé calcule_si_prop_non_nulle_). Car sinon, imaginons un calcul qui au départ se passe dans le domaine F_1 => les lois LOI_TU et LOI_TP accumulent des incréments de contrainte tandis que LOI_TB rien du tout. Et si tout à coup, on passe dans le domaine F_2, voire même carrément purement LOI_TB (F_1 = 0, F_2 = 0) et en très grande déformation, on aurait une loi LOI_TB qui sera le résultat de l'accumulation de un seul incrément de contrainte.
donc, j'ai une loi de mélange qui calcule ses 3 lois à chaque pas de temps. Et qui fait le mélange entre 2 de ses contributions selon leur valeur actuelle.
2) conséquence du point 1), à chaque incrément, 2 lois sont concernées et l'équilibre mécanique va s'établir selon ces 2 lois (convergence vers un certain incrément de déformation DEPS). Mais cet incrément DEPS va également s'appliquer à la 3ème loi qui n'est pas du tout concerné par le processus de recherche d'équilibre. Donc l'incrément qu'elle va accumuler n'a aucun sens mécaniquement parlant. Et si au cours du calcul, le paramètre de mélange vient activer cette 3ème loi, alors on obtient une contrainte aberrante.
Ce problème 2) n'est pas très important sur un trajet monotone. Il est même absent théoriquement. Mais dans un vrai calcul de structure, même si on applique les chargements linéairement, chaque point matériel ne suit pas strictement un trajet monotone. Il va donc y a voir un problème, sans doute pas trop important, mais néanmoins possible. ça reste une faille.
Lorsque l'on fait des trajets volontairement compliqués pour mettre en évidence le problème, on montre facilement que le comportement devient anormal.
exemple ci-dessous sur un quadrangle que je soumet est des changements de trajets en imposant des déformations selon X et Y :
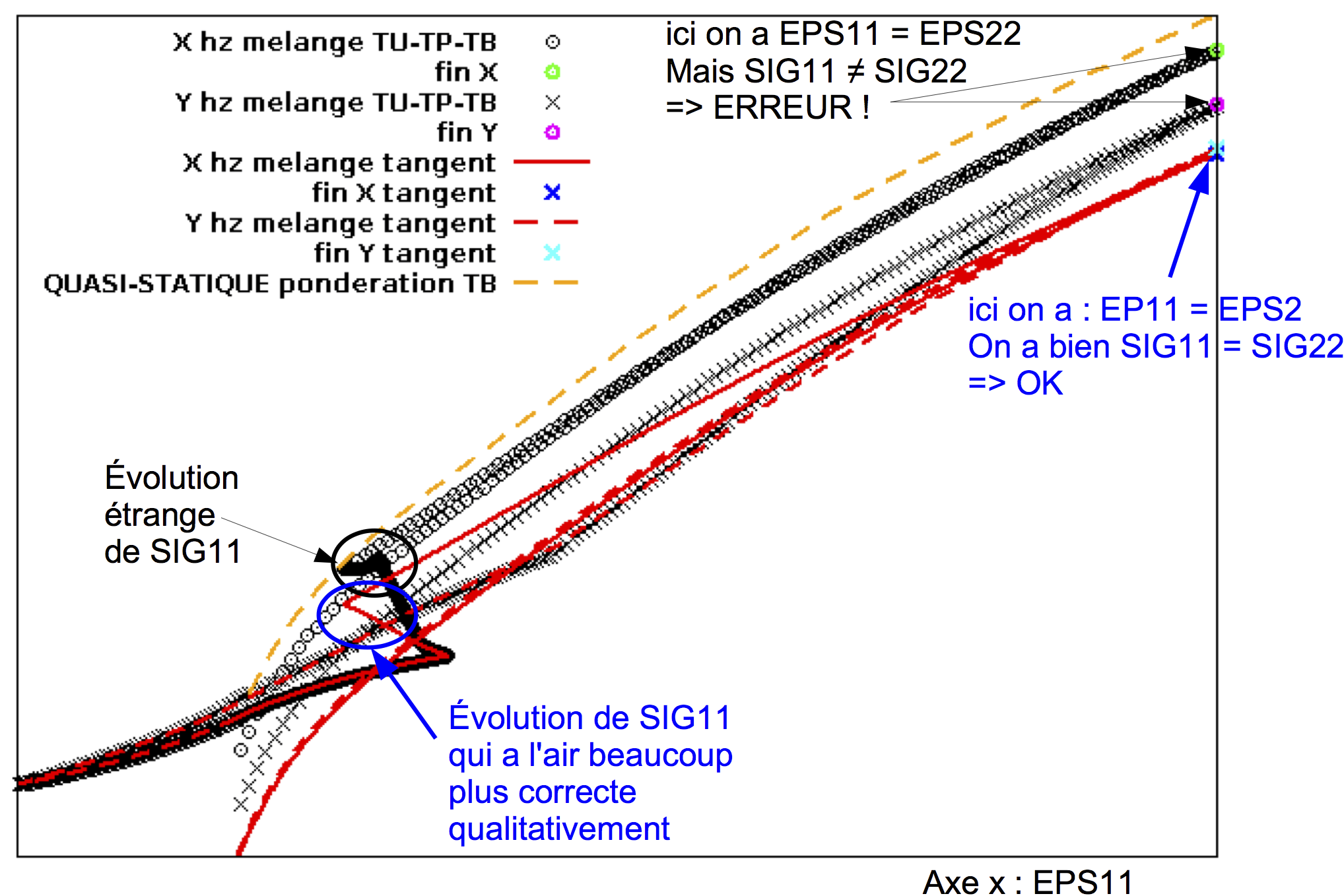
La figure est une peu compliquée. Sans tout expliquer, elle représente l'évolution de la contrainte SIG11 (selon X) et SIG22 (selon Y) en fonction de EPS11. Les points noirs concernent la loi de mélange à 3 lois décrit précédemment. Et la courbe rouge est une loi qui utilise le même principe de mélange mais cette fois, j'utilise une seule loi HYPOELAS et je fais le mélange pour obtenir un Kc tangent et mu tangent en utilisant les mêmes fonctions nD. Cette loi rouge est notée "tangent" dans la légende.
J'ai mis en évidence 2 endroits assez parlant :
1) à gauche, on voit que la loi noire a un espèce de rebroussement de la contrainte en cours de chargement tandis que la loi rouge a une évolution plutôt monotone qui parait bien plus cohérent.
2) à droite, l'état de déformation est exactement équibiaxial EPS11=EPS22. Donc normalement, si la loi ne dépend pas de l'histoire, on doit trouver une contrainte SIG11=SIG22. C'est le cas avec la loi rouge "tangent" mais pas du tout avec la loi noire. Et c'est certainement à cause de la conséquence n°2 que j'ai expliqué plus haut (accumulation d'incréments de contrainte aberrants sur la 3ème loi non activée par le mélange)
et pour finir, très important :
la courbe orange représente le comportement théorique de ce modèle si on avait un chargement purement monotone de traction équibiaxiale. ça permet de mettre en évidence la forte dépendance au trajet des lois HYPOELAS. Tout à droite du graphique, l'état de déformation est équibiaxial. La loi rouge "tangent" est qualitativement correcte : SIG11=SIG22. Mais quantitativement, ce n'est pas bon. La contrainte obtenue après de sévères changements de trajet est bien inférieure au cas orange purement monotone.
conclusion de cette dernière remarque : je veux remplacer les lois HYPOELAS par des lois ISOELAS qui ne dépendent pas du trajet. C'est pourquoi j'ai créé ce ticket. Je veux faire une loi sigma = C(epsilon):epsilon à la place d'une loi sigma_point = C(epsilon):epsilon_point
Mis à jour par Gérard Rio il y a 6 mois
- % réalisé changé de 20 à 30
Bonjour Julien,
je crois avoir compris un peu le pb:
- lorsque l'on active une nième loi hypo, on récupère sa contrainte locale cumulée qui peut éventuellement n'avoir pas de sens avec celle actuelle (globale)...
Informatiquement j'ai l'impression que c'est un comportement normal, par contre d'un point de vue physique on peut effectivement obtenir des discontinuités bizarres !
Concernant spécifiquement les lois hypo, dans le cas d'une loi des mélanges ou d'une loi somme (pondérée ou non):
- au moment de l'appel de la loi hypo, la loi des mélanges transmet à la loi hypo la contrainte (de la loi hypo) au temps précédent.
- la loi hypo calcule l'incrément et l'ajoute à la contrainte précédente, pour obtenir la contrainte finale
- la loi hypo ne stocke pas en interne la contrainte qu'elle a calculée
Donc si on veut assurer une continuité, une idée pourrait-être de transmettre à la loi hypo de base, une contrainte initiale qui satisfait la continuité au temps t.
Si on utilise une loi des mélanges sur les incréments de contraintes, j'ai l'impression que tu aurais directement la continuité ?
OK pour le point 2) de ton précédent message.
Mis à jour par Julien Troufflard il y a 6 mois
Donc si on veut assurer une continuité, une idée pourrait-être de transmettre à la loi hypo de base, une contrainte initiale qui satisfait la continuité au temps t.
je ne pense pas que ce soit la peine de passer du temps à modifier cette loi. Actuellement, le mieux est de faire ce que tu dis après :
Si on utilise une loi des mélanges sur les incréments de contraintes, j'ai l'impression que tu aurais directement la continuité ?
le mélange sur les incréments de contrainte correspond à ce que je fais avec ma 2ème version de loi => les courbes rouge "tangent" sur ma figure. C'est effectivement la moins mauvaise approche.
Pour conclure sur ces travaux, je voudrais juste réussir à produire correctement une loi ISOELAS log, qui viendra remplacer les lois hypo. Et en rester là, car tout ça est un moyen rudimentaire de faire de l'élasticité non linéaire. ça ne devrait pas remplacer une bonne loi hyperélastique.
je vais rédiger le document sur les lois hypo - isoelas. à suivre par mail...
Mis à jour par Julien Troufflard il y a 6 mois
- Fichier test_log_CUsuiviCS.tar test_log_CUsuiviCS.tar ajouté
Comme évoqué plus haut, j'ai voulu vérifier la loi log sur le test "compression uniaxiale (CU) suivi de cisaillement simple (CS)". Mais pas moyen de le faire tourner. ça fait un moment que je tourne autour de mon .info.
ci-joint mon calcul si tu veux regarder. Il y a forcément un truc qui m'échappe.
principe du test :
- un cube 1x1x1 en compression uniaxiale selon Y
- puis (suite_point_info_) cisaillement simple dans le plan XY selon X avec des BLOCAGE_RELATIF_
le tout géré par des TEMPS_MINI et TEMPS_MAXI pour enchainer les 2 sollicitations
le fichier joint crée le répertoire test_log_CUsuiviCS/
je vais avancer sur le doc à t'envoyer par mail
Mis à jour par Julien Troufflard il y a 6 mois
suite message précédent (j'ai oublié de préciser ce qui ne fonctionne pas sur mon calcul)
Le calcul va jusqu'au bout mais le cisaillement ne se produit pas. Le cube subit correctement la compression uniaxiale jusqu'au temps de 1. Puis, il se passe plus rien jusqu'au temps 2.
Mis à jour par Julien Troufflard il y a 6 mois
pour info, je viens de trouver une erreur dans ma loi ISOELAS log. Maintenant elle donne le même résultat que ma loi HYPO. Donc je ne sais pas si c'est la peine que je continue à rédiger le doc à t'envoyer par mail.
Cependant, je resterais preneur d'une réflexion plus large sur comment bien formuler une loi d'élasticité non linéaire (hors hyperélasticité). Pas évident d'en discuter ici ou par mail. Trop long à expliquer. Je suis à peu près sûr que mon approche n'est pas vraiment correcte et qu'il y a moyen de faire mieux.
Si tu es là mardi, on pourra peut-être commencer à en parler rapidement. Je vais voir si je persévère à te rédiger un doc comme base de discussion.
bon week-end
Mis à jour par Gérard Rio il y a 6 mois
oui c'est normal, car par défaut la courbe de chargement générale démarre à 0, puis augmente jusqu'à 1 pour le temps t=1 puis reste constante.
donc la condition:
NdpiY 'UX= 0.3' TEMPS_MINI= 1.000001 BLOCAGE_RELATIF_
va rester constante
Si tu veux avoir une rampe de t=1 à 2, il faut mettre une fonction ou une courbe sur la condition, ou idem sur le type de chargement.
Mis à jour par Julien Troufflard il y a 6 mois
- Fichier TU_CS.png TU_CS.png ajouté
- Fichier chargement_severe.png chargement_severe.png ajouté
- Fichier chargement_severe.info chargement_severe.info ajouté
merci pour le .info.
la dernière version 7.055 converge très bien et donne un résultat parfait en comparaison de la loi élasticité théorique. J'ai comparé à une version antérieure (au hasard la 7.040).
notation :
- TU : traction uniaxiale
- CU : compression uniaxiale
- CS : cisaillement simple
Je regarde les contraintes principales (plus facile à calculer théoriquement dans le cas log). J'utilise une loi E=100, NU=0.3
Voici les résultats :
1) si je fais CU suivi de CS, la version 7.040 donne le bon résultat en CU mais ne converge pas dès le début de la phase CS. La version 7.055 est ok du début à la fin. Je ne montre pas le résultat ici (voir test suivant qui sera plus parlant)
2) même genre de test que précédent mais en faisant TU suivi CS. Les 2 versions hz++ convergent jusqu'au bout mais résultat non correct avec 7.040 comme montré ci-dessous :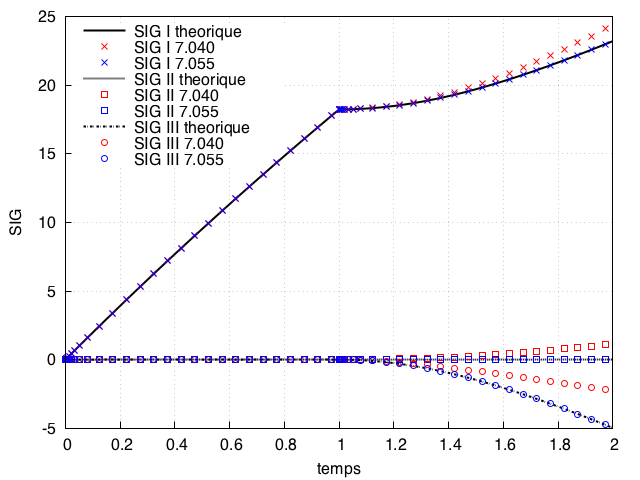
3) dernier test en reprenant le trajet très sévère du message précédent concernant les lois mélange (calcul divisé en 4 phases avec changement de trajet à chaque fois => j'ai mis le .info en pièce jointe si besoin). La direction 3 est libre de contrainte (équivalent d'un calcul membrane contrainte plane).
Résultat ok avec version 7.055 :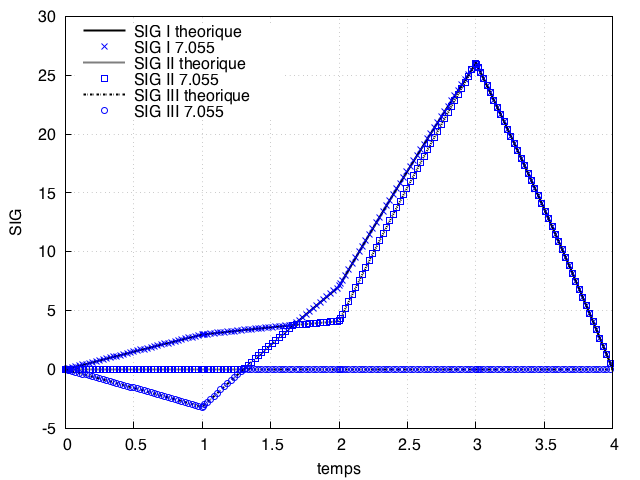
à noter que la version 7.040 ne converge pas jusqu'au bout. Par contre, si j'inverse le signe dans ECHELLE des déplacements imposés X et Y, les 2 versions convergent et donnent le résultat théorique.
Mis à jour par Julien Troufflard il y a 6 mois
- Fichier chargement_severe_EPS33.png chargement_severe_EPS33.png ajouté
suite test 3) précédent
Vérification de la déformation 33 (NU=0.3) => OK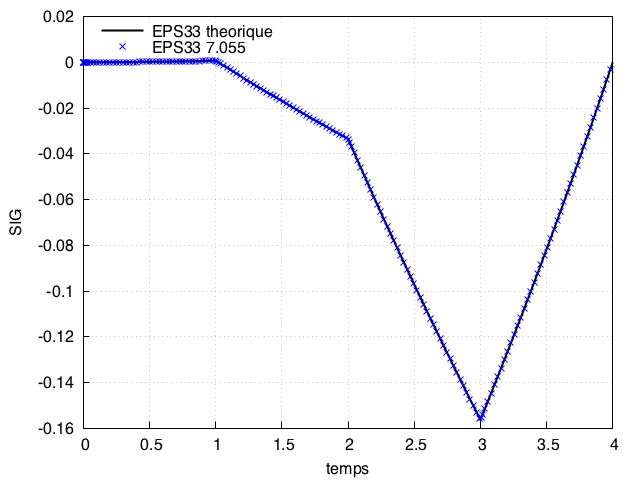
Mis à jour par Julien Troufflard il y a 5 mois
ok pour ce ticket.
En conclusion :
1) en attente d'une version contrainte plane
2) suite discussion hier, je me dis que peut-être une version HYPOELAS en calcul sécant serait quand même intéressante en terme de temps de calcul par rapport à ISOELAS log.