Anomalie #360
ouvertnon convergence pour MAHEO_HYPER et HYPER_EXTERNE_W
Description
Gérard,
je suis tombé sur un cas de non convergence inattendu pour des lois MAHEO_HYPER et HYPER_EXTERNE_W.
Dans le repertoire joint, j'ai mis un calcul de traction sur un cube.
Toutes les lois présentes dans le .info convergent si on met une condition de déplacement imposé.
Par contre, les lois MAHEO_HYPER et HYPER_EXTERNE_W divergent si je mets une contrainte imposée (chargement PRESSION sur une face pour atteindre 60 MPa).
je ne comprends l'origine de cette divergence. Toutes les lois proposées dans le .info sont capables de fournir une contrainte de 60 MPa. Elles convergent d'ailleurs toutes en déplacement imposé très grande déformation (def log 1.5) et atteignent une contrainte au moins égale à 60 MPa.
Je ne pense pas que cela vienne particulièrement du choix d'un modèle en invariant de B puisque la loi Mooney Rivlin converge très bien ainsi que la loi MAT_maheoHyper_lineaire (modèle sans seconde pente).
est-ce que ça vient de la forme du comportement ? MAT_Favier converge pourtant très bien et j'ai fait en sorte que les lois MAT_Favier, MAT_maheoHyper, hyper_externe_W soient assez semblables (en traction) comme montré sur ce graphe :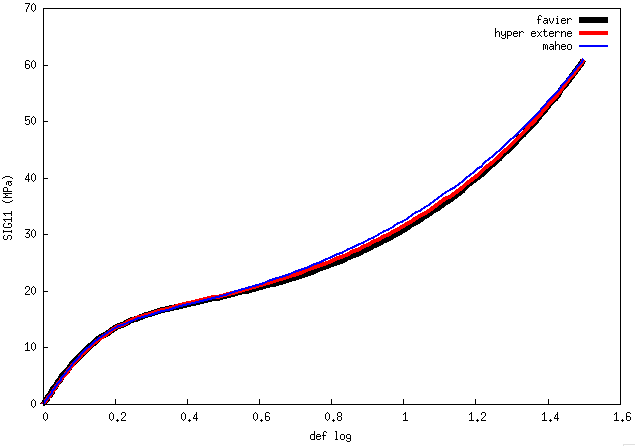
mais je vois bien que la loi MAT_maheoHyper_lineaire converge très bien. Il s'agit d'une loi assez linéaire de type MAHEO_HYPER.
Donc que penser de tout ça...
j'ai mis un Readme avec d'autres infos.
a+
Julien
Fichiers
Mis à jour par Julien Troufflard il y a plus de 2 ans
ps : pour situer un peu par rapport au graphe du message précédent, la loi MAT_maheoHyper diverge en contrainte imposé vers une déformation log de 0.7
Mis à jour par Julien Troufflard il y a plus de 2 ans
... et pour la loi MAT_hyperExt, la divergence intervient vers une def log de 1.06
Mis à jour par Julien Troufflard il y a plus de 2 ans
et dernier ps : ça n'a pas l'air sensible au facteur de régularisation. Pour le loi MAT_maheoHyper, j'ai testé 1e-14, 1e-10, 1e-6 et même 1e-4 et 1e-1 => divergence toujours à peu près au même endroit
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier cpt_compression_Favier.png cpt_compression_Favier.png ajouté
en fait, on retrouve le même genre de divergence avec la loi MAT_Favier si on impose cette fois une contrainte de compression de -60 MPa.
La divergence a lieu vers une déformation log de -0.4. Vu la forte dissymétrie traction/compression, le comportement en compression uniaxiale de cette loi Favier est le suivant :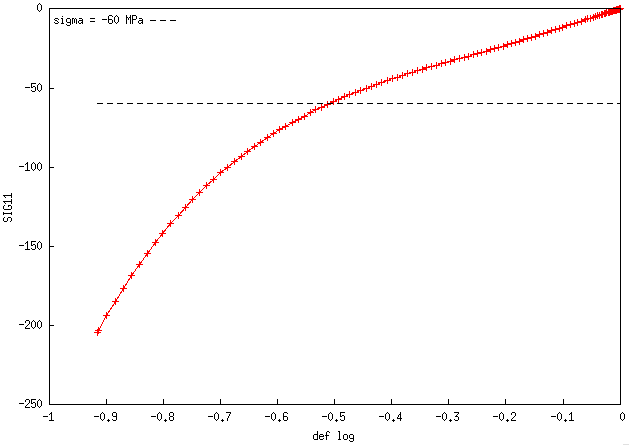
et j'ai cherché à atteindre -60 MPa. Pas de non linéarité particulière sur ce domaine et normalement aucun problème pour atteindre ce niveau de contrainte. La loi converge très bien en déplacement imposé (ce qui a permis de tracer ce graphe).
je ne comprends vraiment pas. On dirait que c'est plus lié au mode de chargement qu'à la loi en elle-même. Mais néanmoins, certaines lois convergent très bien => en gros les lois assez linéaires de type : mooney-rivlin, maheo sans seconde pente, hypo elastique.
autre chose curieuse : même une loi ISOELAS peut être mise en échec.
par exemple la loi suivante :
MAT_isoelas ISOELAS
200 0.49
elle diverge très tôt vers une déformation log de -0.11 en contrainte imposée. Elle converge assez bien en déplacement imposé même si elle n'arrive pas à dépasser une def log de -0.55 (soit une contrainte de compression de l'ordre de -200 MPa).
de même en traction, elle converge très bien en déplacement imposé mais diverge vers une déf log de +0.12 en contrainte imposée.
Pour rappel, son analogue HYPO_ELAS E=200 NU=0.495 converge très bien en traction/compression que ce soit en contrainte imposé ou déplacement imposé très (très) grande déf.
La loi mooney-rivlin également présente dans le .info montre la même robustesse.
peu importe le chargement, ces 2 lois convergent toujours.
je ne comprends pas le point commun qui conduit les diverses lois à diverger. Et de même, le point commun entre les lois qui sont robustes.
Mis à jour par Julien Troufflard il y a plus de 2 ans
si j'augmente assez le chargement avec les lois supposées robustes (mooney-rivlin, hypoélastique), j'arrive toujours à trouver une contrainte telle que le calcul diverge. Donc en fait toutes les lois peuvent potentiellement être mise en défaut.
c'est donc commun à toutes les lois. Je pense que la face soumise au chargement doit vouloir vriller (le chargement est suiveur)
Si je mets des conditions linéaires de manière à imposer à la face X de rester droite (même UX sur ses noeuds), les calculs convergent.
(et logiquement je devrais faire de même pour les autres faces : noeuds face Y => même UY et noeuds face Z => même UZ)
Gérard, pas sûr qu'il faille dépenser de l'énergie sur ce ticket. A l'origine, c'est un autre problème que je souhaitais te soumettre et qui dépendait de la réussite de calculs en contrainte imposée.
Mis à jour par Julien Troufflard il y a plus de 2 ans
- Fichier test.info test.info ajouté
- Fichier TU_CU_Favier.png TU_CU_Favier.png ajouté
- Fichier TU_CU_isoelas.png TU_CU_isoelas.png ajouté
- Fichier TU_CU_isoelas_hyperBulk.png TU_CU_isoelas_hyperBulk.png ajouté
Epilogue :
mon but est de comprendre ce qui peut nuire à la convergence d'une loi de comportement. Pour finir avec ce ticket, voici quelques précisions.
j'ai modifié le .info de manière à imposer aux faces libres du cube de rester droites dans leur direction respective (nouvelle version en pièce jointe). De cette manière, je pense m'être affranchi des artefacts numériques conduisant le cube à vriller sous l'action du chargement suiveur. Ceci pour étudier purement la loi de comportement.
Une raison principale de la divergence d'une loi est d'atteindre un stade où le coefficient de poisson apparent NU devient non physique. Le coeff de poisson apparent est pour moi la grandeur :
NU = - delta(def log 22) / delta(def log 11)
pour une sollicitation uniaxiale dans la direction 11 (delta = incrément de déformation entre 2 incréments)
Le coeur du problème est je pense que la stabilité d'un calcul dépend notamment du fait que NU appartienne à l'intervalle ]-1:0.5[. La borne -1 pourrait être associée au cisaillement => si NU est inférieur à -1, le module de cisaillement G (apparent) deviendrait négatif. Et de même pour la borne +0.5, s'il dépasse 0.5, le module de compressibilité K (apparent) deviendrait négatif.
Si on trace le comportement traction(TU)-compression(CU), on a :
pour MAT_Favier :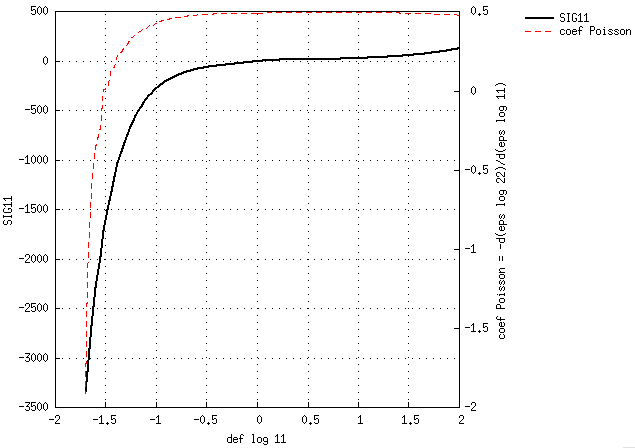
pour MAT_isoelas :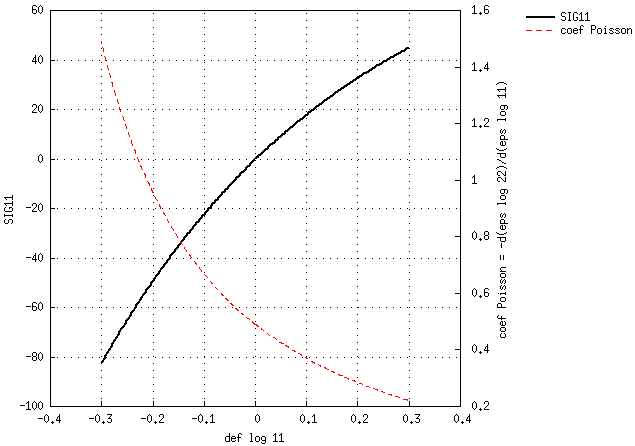
pour ces 2 lois, par le test en CU, j'arrive à atteindre une contrainte imposée de plus de -3000 MPa pour Favier et de seulement -24 MPa pour isoelas. Dans les 2 cas, le coef de Poisson apparent est passé hors bornes depuis un moment.
Chose intéressante, si on reprend une loi isoelas, mais que l'on garde uniquement sa partie déviatorique et que l'on additionne à un ISOHYPERBULK de module de compressibilité équivalent à la loi élastique (E=200, NU=0.49 => K = 3333.333 => isohperbulk => 3K = 10000), on obtient le comportement TU-CU suivant :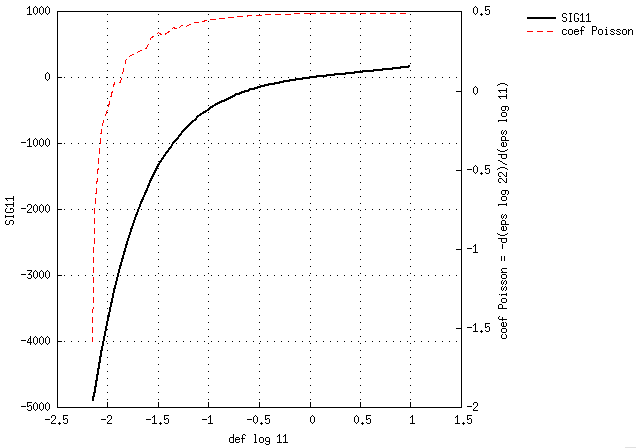
c'est le matériau MAT_soelas_hyperBulk dans le fichier test.info joint.
et avec cette nouvelle version de loi isoelas, je peux pousser le chargement de contrainte imposée à -4000 MPa.
en compression, il y aurait donc une relation directe entre coef de poisson apparent et possibilité de convergence.
Par contre, la chose que je ne comprends pas, c'est que avec la loi isoelas de base, le calcul diverge en traction pour un contrainte imposée d'environ +20 +25 MPa. Le coef de Poisson est pourtant encore largement dans les clous d'après la 2ème figure ci-dessus, même s'il évolue très vite (NB : pour tendre vers 0).
Cette histoire de compressibilité est centrale dans la convergence des lois LOIS_CONTRAINTES_PLANES.
Je regarde actuellement les possibilités de pilotage de la loi d'Orgeas avec l'angle de Lode et les histoires de non convexité du potentiel. Mais avant ça, même pour un potentiel convexe (le potentiel de Favier est convexe par rapport à Qeps), on peut trouver des cas de divergence du simple fait de la compétition entre la partie déviatorique et la partie sphérique (coef de Poisson apparent).
De plus, si la compressibilité de la loi n'est pas bien définie, il y a également des difficultés. C'est le cas de ISOELAS dont la partie sphérique n'a plus de sens si on est en grande déf.
Mis à jour par Gérard Rio il y a plus de 2 ans
- Statut changé de Nouveau à En cours
- % réalisé changé de 0 à 50
Je crois que la non-convergence vient du fait que la raideur par défaut (dans Herezh) est traitée comme symétrique. Cela permet classiquement d'avoir une convergence rapide (quadratique) et un stockage faible.
Dans le cas d'une grande déformation (et également avec des forces suiveuses) on obtient une raideur globale non symétrique en particulier due à la variation du jacobien. Du coup, avec la résolution par défaut qui utilise (par défaut) un stockage symétrique il y a un moment où ce n'est plus suffisant pour obtenir une solution unique.
Aussi, la solution est d'utiliser un stockage non symétrique et une résolution qui respecte cette non-symétrie.
Dans Herezh tu peux utiliser les paramètres suivants:
- PARAMETRE | VALEUR |
#-----------------------------------------------
TYPE_MATRICE BANDE_NON_SYMETRIQUE_LAPACK
SYMETRIE_MATRICE 0
TYPE_RESOLUTION GAUSS
para_syteme_lineaire ------------
#-----------------------------------------------Avec ces paramètres, toutes les lois que tu as proposées fonctionnent jusqu'à la pression maxi que tu as indiqués.
Si tu as une pression importante, certaines fois il est intéressant de compléter la raideur locale par un terme qui dépend de la variation de la direction du chargement (c-a-d liée à la force suiveuse).
Pour cela il faut utiliser dans les paramètres de contrôle général:
VARIATION_CHARGE_EXTERNE_SUR_RAIDEUR 1
Enfin un point important, il faut veiller à ce que la partie volumique (qui conduit à la partie sphérique du tenseur des contraintes) de la loi de comportement ne soit pas trop "très très" différente de la partie déviatorique. Ce n'est pas le cas dans les lois que tu proposes, mais je le rappelle pour ceux qui liront ma réponse.
Par exemple si la partie volumique est très très grande, elle "écrase" la partie déviatorique et la raideur devient singulière.
Cela ne rend pas caduques tes investigations qui sont pertinentes.
Mis à jour par Julien Troufflard il y a plus de 2 ans
ah oui effectivement c'est radical avec les options TYPE_MATRICE etc... il n'y a plus besoin de conditions linéaires. C'était bien le défaut majeur dans mes calculs.
Le paramètre VARIATION_CHARGE_EXTERNE_SUR_RAIDEUR n'a pas d'influence a priori sur ce cas mais intéressant de le savoir (à tester sur des cas de membrane sous pression solvable en implicite, comme un bulge-test par exemple).
la prise en compte de la non-symétrie résout complètement le cas ISOELAS (pas de divergence en traction et il faut vraiment beaucoup charger en compression pour atteindre la divergence).
De mon analyse, il ne reste de valide que le franchissement de la borne -1 sur le coef de Poisson apparent. J'ai testé uniquement Favier. Je ne peux pas augmenter le chargement au-delà de ce que j'avais déjà réussi à obtenir en compression (-3000 MPa environ, soit un stade où le coef devient inférieur à -1).
En revanche pour ISOELAS, on peut aller très loin en compression avec un coef Poisson apparent de l'ordre de 6 voire 7. La convergence semble bien tolérer un très gros coef de Poisson non physique.
Merci pour le vrai correctif qui manquait à mon .info.
Globalement ok pour moi sur ce ticket. Avec toutefois une dernière question :
est-ce que les options sur la non-symétrie de matrice peut avoir un quelconque impact sur l'amélioration de la convergence d'une loi contrainte plane ? surement que non, mais après tout, il s'agit de résoudre une équation sigma_33 = 0, ce qui pourrait être analogue à imposer un chargement qui a une direction du point de vue de la loi 3D, mais je m'égare sans doute...
Mis à jour par Gérard Rio il y a plus de 2 ans
- % réalisé changé de 50 à 90
Dans le cas des contraintes planes, c'est une matrice 1x1 qui est utilisée donc il n'y a pas de dépendance à la symétricité (cf. LoiContraintesPlanes.cc).
Par contre, effectivement dans le cas des contraintes planes doubles, c'est une matrice 2x2 qui est utilisée et elle est non symétrique
(ex. LoiContraintesPlanesDouble.h ligne 472:
MatLapack der_at_racine;
et j'utilise une matrice carrée non symétrique avec un stockage lapack et une résolution de GAUSS. Ex. LoiContraintesPlanesDoubles.cc ligne 293, au niveau du contructeur :
,der_at_racine(2,2,false,0.,GAUSS,RIEN_PRECONDITIONNEMENT)
Mis à jour par Gérard Rio il y a plus de 2 ans
- Statut changé de En cours à Résolu
- % réalisé changé de 90 à 100