Assistance #362
ouvertsorties loi HYPO_ELAS2D_C
Ajouté par Julien Troufflard il y a environ 2 ans. Mis à jour il y a environ 2 ans.
Description
Bonjour Gérard,
je voudrais faire évoluer Kc et mu en fonction IIeps pour une loi HYPO_ELAS2D_C.
J'ai voulu regarder si la loi donnait accès à IIeps en sortie. J'ai cru comprendre que IIeps était le produit double contracté EPS:EPS, donc la norme au carré du tenseur de déformation Almansi complet (i.e pas seulement la partie déviatorique).
Je pourrais calculer EPS:EPS moi-même en sortie mais je préfèrerais voir celui qui réellement utilisé par la loi (en particulier dans le cas présent qui concerne les éléments membrane). Je n'ai pas trouvé comment avoir cette grandeur.
La doc Herezh dit que pour une loi HYPO_ELAS2D_C, on peut obtenir en sortie :
MODULE_COMPRESSIBILITE
MODULE_CISAILLEMENT
DEF_EPAISSEUR
DEF_ASSO_LOI
J'ai deux demandes :
1) a priori il n'y a pas IIeps en sortie, est-il possible de l'avoir ?
2) je n'ai pas trouvé les grandeurs en sortie (MODULE_COMPRESSIBILITE, etc...). Plus précisément, je m'attends à ce qu'elles figurent dans "grandeurs particulières éléments" (choix "elp" dans le menu interactif CVisu). J'obtiens effectivement toutes les grandeurs prévues si j'utilise une loi 3D HYPO_ELAS3D encapsulée dans une loi contrainte plane. Mais rien pour une loi HYPO_ELAS2D_C.
Est-ce possible de les rendre accesibles ? y compris IIeps ?
J'ai joint une archive avec un exemple en traction sur un quadrangle avec au choix un loi 2D et une 3D contrainte plane.
J'ai mis également l'affichage Herezh du menu interactif aux choix "elp" en sortie maple pour créer le .CVisu.
Dans le cas HYPO_ELAS3D + contrainte plane, j'obtiens bien :
Mais dans le cas HYPO_ELAS2D_C, je n'ai pas les sorties attendues :
j'ai cherché ailleurs dans le menu interactif, sans succès.
a+
Julien
Fichiers
Mis à jour par Julien Troufflard il y a environ 2 ans
j'y pense après coup. La grandeur IIeps, si elle est liée à Almansi ne sera pas identique en traction et compression à niveau de déformation log équivalent => par exemple : IIeps(def_log = 0.4) différent de IIeps(def_log = -0.4).
Je voudrais faire une loi HYPOELAS avec des coefficients Kc et mu qui varient mais tout en restant "symétrique" traction/compression du point de vue log.
Comment piloter les coefs pour obtenir ça ? Est-ce possible d'avoir un équivalent IIeps mais en déformation log ? (le tout sans oublier que c'est pour des membranes, donc il faut tenir compte de la déformation d'épaisseur)
Mis à jour par Gérard Rio il y a environ 2 ans
- Tracker changé de Anomalie à Assistance
Bonjour Julien,
quelques infos:
- Dans Herezh la norme au carré de la déformation est représentée par II_eps = eps:eps et celle du déviateur : II_eps_barre = eps_barre : eps_barre
- Lorsqu'on calcule la loi de comportement à un pti (cf. pres_developpeur.pdf dispo également sur le site d'Herezh dans le projet partie développeur) on appelle Loi_comp_abstraite qui ensuite appelle la loi spécifique. Avant l'appel de la loi spécifique, on calcule "éventuellement" 3 invariants principaux de la déformation et de la vitesse de déformation (cf. méthode CalculInvariants_cinematique) :
switch (abs(dimT))
{case 3: invariant(3)= epsHB.Det();
case 2: invariant(2)= epsHB.II();
case 1: invariant(1)= epsHB.Trace();
};ou dimT est la dimension du tenseur : ex: en dim 2 on calcule la trace d'eps et la trace de eps . eps, et en dim 1 seul la trace d'eps est calculée. Les grandeurs sont ensuite disponibles au niveau de la loi spécifique.
Donc a priori on peut rendre accessibles directement ces grandeurs.
- dans le cas de l'utilisation de la déformation d'Almansi, les valeurs limites de la déformation sont différentes en traction et compression donc on aura la même chose pour les invariants. Si on veut des limites équivalentes en traction et compression une solution est d'utiliser une déformation log ou log cumulé.
Dans le cas de la loi hypo_elas_2D_C (cf. fichier Hypo_hooke_2D_C.cc) on utilise l'incrément de déformation et une déformation cumulée en 2D, qui représentent ce qui est constaté cinématiquement dans le plan. On peut accéder à ces grandeurs via (3 composantes) le mot clé "DEF_ASSO_LOI"
- la déformation d'épaisseur dépend du coefficient de compressibilité "global". En particulier si on utilise une loi combinée c'est le coefficient de compressibilité résultant de l'application de toutes les lois élémentaires, qui doit-être utilisé.
Dans Herezh j'ai mis un mécanisme qui permet de transmettre aux lois élémentaires, des infos qui ne sont connues qu'au niveau supérieur. On pourrait donc utiliser ce mécanisme pour transmettre le coef de compressibilité global à la loi hypo elas 2D_C. Par contre il faut noter que ce sera une info de l'itération précédente, car la globalisation de la compressibilité s'effectue après le calcul des lois élémentaires. Si on a convergence, c'est ok, mais cela peut impacter la convergence si l'influence de la déformation d'épaisseur est importante dans la loi élémentaire...à voir dans des tests d'application.
- sortie du module de compressibilité: normalement tu devrais pouvoir utiliser le mot clé "MODULE_COMPRESSIBILITE" avec la loi hypo_elas_2D_C (cf. fichier Hypo_hooke_2D_C.cc, méthode: Hypo_hooke2D_C::Grandeur_particuliere). Je vais refaire ton test et te tiens au courant
Mis à jour par Gérard Rio il y a environ 2 ans
- Statut changé de Nouveau à En cours
- % réalisé changé de 0 à 50
Mis à jour par Gérard Rio il y a environ 2 ans
J'ai trouvé une boulette qui explique le fait que certaines grandeurs n'étaient pas dispo: ça, c'est maintenant ok tu vois toutes les grandeurs et tu peux les sortir. J'avais fainéanté en utilisant une méthode virtuelle avec init pas défaut (et pour cette méthode uniquement ! j'avais oublié un paramètre ce qui conduisait à l'utilisation de l'init par défaut )... certaine fois il vaut mieux une virtuelle pure qui est beaucoup plus sûr !
Par contre je vois un souci pour la sortie des def cumulées qui s'effectue en 2D (car calculé en 2D) et je suis en espace 3D via un repère ad hoc ou pas et j'ai une embrouille au niveau du passage... bon ce n'est pas méchant mais il faut que j'ai les idées un peu plus claires que ce soir,
je regarde et te tiens au courant.Mis à jour par Julien Troufflard il y a environ 2 ans
merci Gérard.
Je vais poser une autre question dans un autre ticket. C'est lié à ce ticket mais d'un sujet trop différent pour l'inclure ici.
Mis à jour par Gérard Rio il y a environ 2 ans
- % réalisé changé de 50 à 80
c'est ok, pour la sortie des def cumulées. Bien noter que si on demande une sortie par défaut, dans le cas des éléments 2D, les tenseurs sont dans un repère orthonormé ad hoc (cf. doc), dont les 2 premiers vecteurs sont (sauf cas particulier) dans le plan de l'élément, avec le premier vecteur selon x ( sauf cas particulier où I_1 ne peut pas être projeté sur le plan médian). Le troisième vecteur est normal au plan médian et le second complète le repère. Dans le test on a directement la première composante du tenseur selon x et la troisième ( composante (2,2) cf. info dans l'entête du . maple) selon y .
Dans le style de sortie on peut aussi demander une sortie dans le repère globale.
mise à jour dans la version 7.021 à tester
Mis à jour par Julien Troufflard il y a environ 2 ans
- Fichier test_hypo_def_K_G.tar test_hypo_def_K_G.tar ajouté
- Fichier verif_def_epaisseur.png verif_def_epaisseur.png ajouté
- Fichier verif_evolution_K_G.png verif_evolution_K_G.png ajouté
je viens de tester la nouvelle version.
ci-joint un exemple en traction sur un quadrangle pour une loi dont Kc et mu dépendent d'une fonction de II_eps. La fonction est la même sur Kc et mu. On multiplie Kc et mu par un coef 1 en dessous de II_eps = 0.05. Puis le coef multiplicateur passe de 1 à 3 linéairement entre II_eps = 0.05 et 0.1.
Dans l'exemple joint, le fichier gnu_verif_def_K_G trace un premier graphique pour vérifier les déformations DEF_ASSO_LOI, DEF_EPAISSEUR et également, EPAISSEUR_FINALE. Le second graphe montre l'évolution de K et G (MODULE_COMPRESSIBILITE et MODULE_CISAILLEMENT).
Premier graphe :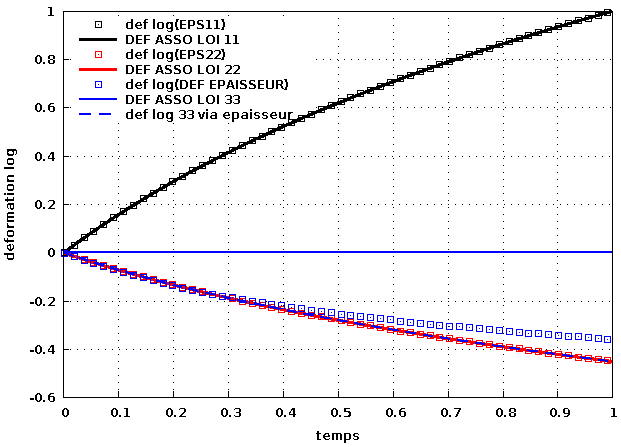
=> conclusion :
1) déformation DEF_ASSO_LOI 11 et 22 (traits et points noirs et rouges) => composantes 11 et 22 ok et conformes à la conversion log de EPS11 et EPS22
2) déformation DEF_ASSO_LOI 33 => elle est nulle (trait bleu)
3) déformation DEF_EPAISSEUR => par isotropie, elle devrait être égale à EPS22 (mesure almansi). Sur la graphe (points bleu), sa conversion log est proche de def_log(EPS22)/DEF_ASSO_LOI 22 au départ mais s'écarte progressivement.
4) EPAISSEUR_FINALE est ok => en pointillé bleu, on voit que le calcul de la def epaisseur 33 via l'épaisseur est ok. On a bien def log 33 = ln(EPAISSEUR_FINALE/0.038) égal à def_log(EPS22)/DEF_ASSO_LOI 22.
Deuxième graphe :
conclusion :
1) ma première interrogation était de voir si le calcul de II_eps tenait compte de la déformation épaisseur. Donc là, on voit que non (cas d'un tenseur 2D membrane : EPS11 EPS22 EPS12, EPSi3=0 i=1,2,3). Le changement de coefficient matériau a bien lieu entre 0.05 et 0.1 avec II_eps tel que EPS33=0
2) la valeur du module de compressibilité est conforme. La grandeur MODULE_COMPRESSIBILITE est le module de compressibilité K=E/(3*(1-2NU))
3) La grandeur MODULE_CISAILLEMENT n'est pas directement le module de cisaillement. Il s'agit cette fois de mu = 2G. Sa valeur est conforme.
Donc au final, c'est surtout DEF_EPAISSEUR qu'il faut vérifier.
De mon côté, je vais voir si je peux piloter la loi avec des fonctions nD en calculant un II_eps mais en mesure log et en tenant compte de EPS33.
Mis à jour par Julien Troufflard il y a environ 2 ans
- Fichier test_Hypo_fct_nD.tar test_Hypo_fct_nD.tar ajouté
en premier test d'une loi HYPO_ELAS2D_C avec fonction nD sur Kc et mu, j'obtiens un message d'erreur :
erreur en lecture du mot cle Kc=
on a lue Kc_fonction_nD:Hypo_hooke2D_C::LectureDonneesParticulieres( ...
je ne trouve pas la bonne syntaxe dans la doc ou avec HZpp -n. J'ai essayé sans succès plusieurs combinaisons avec ou sans sauts de ligne, avec symbole : ou _ dans le mot-clé, avec ou sans valeur scalaire avant Kc_fonction_nD, etc...
ci-joint ma mise en données
Mis à jour par Gérard Rio il y a environ 2 ans
- Fichier clipboard-202401241013-hqvhk.png clipboard-202401241013-hqvhk.png ajouté
- Fichier clipboard-202401241014-kaoc3.png clipboard-202401241014-kaoc3.png ajouté
- Fichier clipboard-202401241014-i2quw.png clipboard-202401241014-i2quw.png ajouté
commentaire sur #7:
"=> conclusion :
1) déformation DEF_ASSO_LOI 11 et 22 (traits et points noirs et rouges) => composantes 11 et 22 ok et conformes à la conversion log de EPS11 et EPS22"
Il faut garder en tête que DEF_ASSO_LOI 11 et 22 correspondent à des def log cumulées donc c'est différent d'une def log exacte, DEF_ASSO_LOI dépend de l'incrément utilisé pour le calcul, plus l'incrément est grand plus on s'écartera d'une def log exacte
"2) déformation DEF_ASSO_LOI 33 => elle est nulle (trait bleu)"
cette déformation n'existe pas pour la loi HYPO_ELAS2D_C, c-a-d elle n'est pas utilisée et donc pas calculée, donc en sortie elle est initialisée à 0
"3) déformation DEF_EPAISSEUR => par isotropie, elle devrait être égale à EPS22 (mesure almansi). Sur la graphe (points bleu), sa conversion log est proche de def_log(EPS22)/DEF_ASSO_LOI 22 au départ mais s'écarte progressivement."
ici il s'agit de la déformation d'épaisseur calculée pour le post-traitement, dans la loi (ce n'est pas une grandeur utilisée pour la loi). D'une manière générale, j'utilise le module de compressibilité pour calculer une variation de volume qui ensuite permet de calculer la variation d'épaisseur. D'où :
a) la variation d'épaisseur que l'on obtient au niveau d'une loi élémentaire peut-être différente de la variation finale dans le cas d'une loi complexe
b) la relation def épaisseur - variation de volume, dépend d'un choix que l'on fait sur la signification du module de compressibilité cf. doc théorique, formule 484, 485, 491. Dans la loi j'utilise (cf. code source): 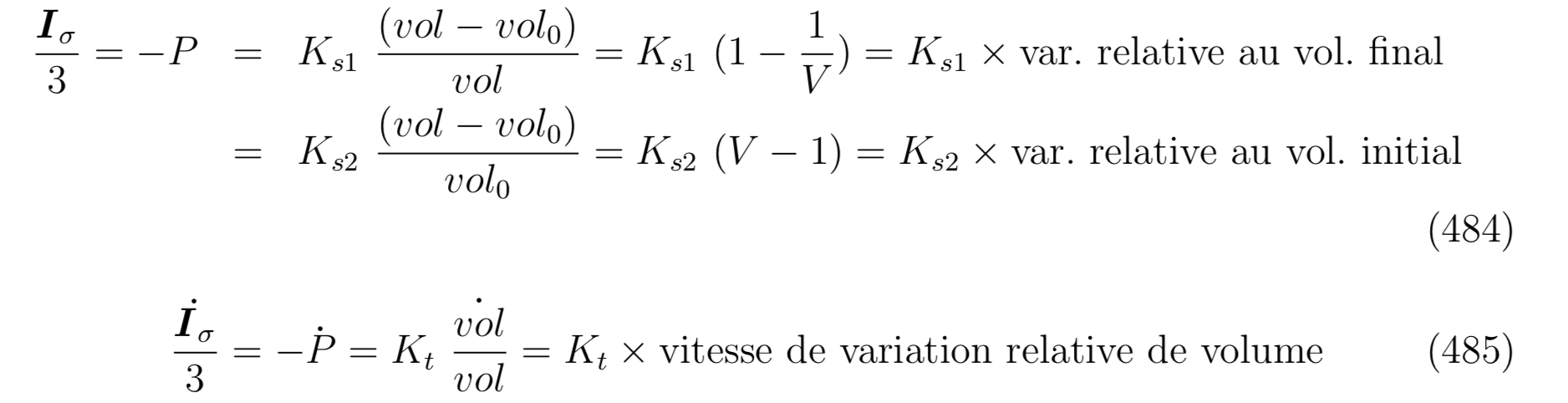
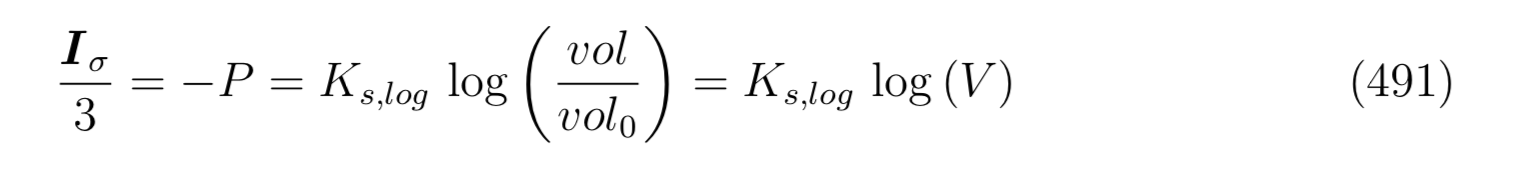
else // sinon le module étant suffisament grand on va pouvoir calculer
{// on pose
double log_var_surf = log(()/((ex.jacobien_0)));
// log (var_vol) = traceSig / 3 / K = log(var_sur) + log(var_epais)
// d'où log(var_epais) = epsBH33 = traceSig / 3 / K - log(var_sur)
save_resul.eps33 = Isigma * untier / Kc_use - log_var_surf;
};
Donc on devrait avoir la bonne variation logarithmique d'épaisseur
"4) EPAISSEUR_FINALE est ok => en pointillé bleu, on voit que le calcul de la def epaisseur 33 via l'épaisseur est ok. On a bien def log 33 = ln(EPAISSEUR_FINALE/0.038) égal à def_log(EPS22)/DEF_ASSO_LOI 22."
a) ici il s'agit de la sortie de l'épaisseur finale calculée au niveau de l'élément fini, via la loi de comportement complète (donc ici on a cumulé toutes les lois individuelles s'il s'agit d'une loi complexe).
b) le calcul est fait en incrémental, il correspond donc à une épaisseur finale via une def log cumulée cf. code source: méthode: QuadraMemb::CalEpaisseurMoyenne_et_transfert_pti,
...
{double epaisseur_moy_tdt = (epaisseur_moy_t * jacobien_moy_ini) / jacobien_moy_fin
* troisK_moy / (troisK_moy - traceSig_moy+traceSig_moy_ini);
...
ce qui correspond à la formule théorique 493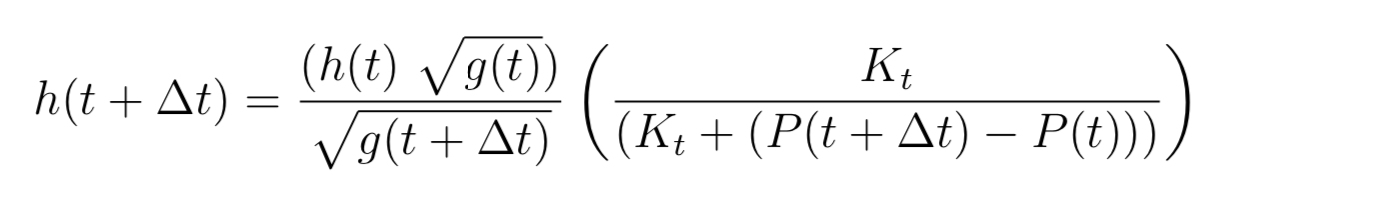
Mis à jour par Gérard Rio il y a environ 2 ans
- % réalisé changé de 80 à 90
Effectivement la lecture des coefficients matériaux avec les lois hypo isotropes (2D, 1D et 3D) avait un pb. Je pense que c'est apparu à la suite de l'inclusion de fct nD dans les hypo ortho, j'ai voulu unifié les lectures, mais en fait il est nécessaire de garder des différences.
- donc: version 7.022 contient la mise à jour qui est conforme au test
- je vais également inclure cette mise en données comme exemple dans la doc
Mis à jour par Julien Troufflard il y a environ 2 ans
- Fichier epsLog_sigC.png epsLog_sigC.png ajouté
- Fichier eps11_eps22_LOG.png eps11_eps22_LOG.png ajouté
impeccable avec version 7.022
j'arrive à faire une loi symétrique traction-compression en mesure log avec des fonctions nD.
Je recalcule un IIeps mais en mesure log et en tenant compte de la déformation d'épaisseur (je la calcule moi-même connaissant les déformations principales I et II et le coef de Poisson).
par exemple, en choisissant un coef poisson 0.4 :
deformation - contrainte => symétrie parfaite traction-compression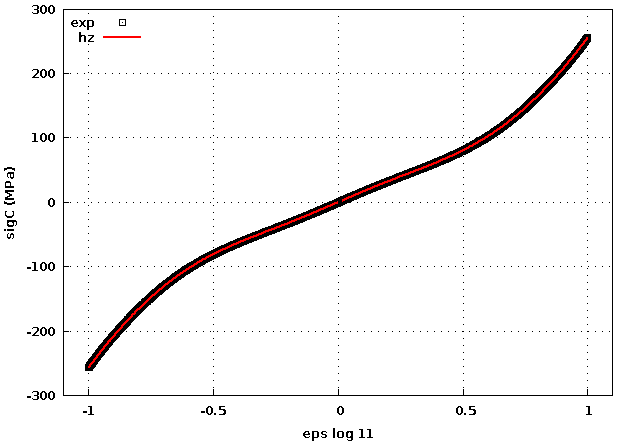
cinématique transverse => coef poisson constant (et toujours symétrie traction-compression)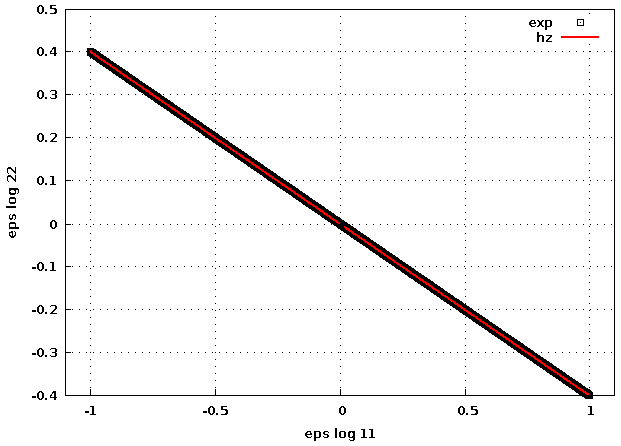
Mis à jour par Julien Troufflard il y a environ 2 ans
- Fichier pas_temps_0p01_epsLog_sig.png pas_temps_0p01_epsLog_sig.png ajouté
- Fichier pas_temps_0p05_epsLog_sig.png pas_temps_0p05_epsLog_sig.png ajouté
- Fichier pas_temps_0p01_eps11_eps22.png pas_temps_0p01_eps11_eps22.png ajouté
j'ai testé en relaxation dynamique => même résultat qu'en non_dynamique
par compte, je me demande si c'est la bonne démarche d'utiliser une loi hypo en relaxation dynamique(RD). En RD, on a tendance à faire des grands pas de temps, et du coup le suivi de la loi ne va pas être bon.
par exemple, même comportement que précédemment, avec un pas de temps 10 fois plus grand (0.01) :
contrainte - déformation : la compression a l'air de poser plus de souci mais ça reste léger pour l'instant
NB : la courbe rouge (non_dynamique) et verte (relaxation dynamique, amortissement cinétique) sont superposées => même pas de temps = même comportement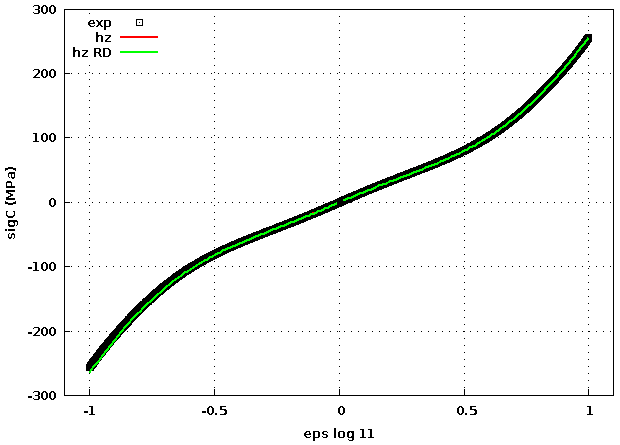
idem mais avec pas de temps 50 fois plus grand (0.05) :
l'écart devient plus visible, toujours la compression qui pose le plus de difficulté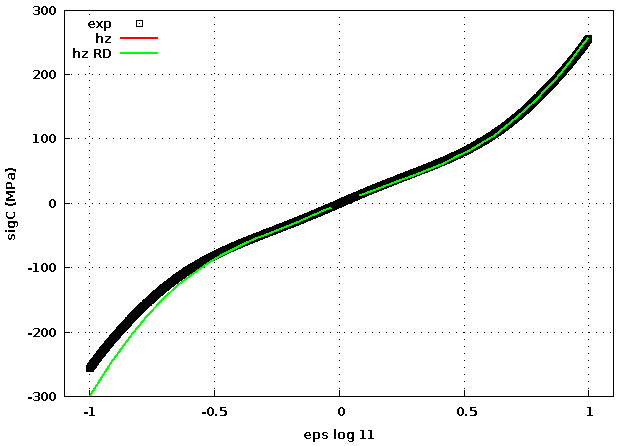
pour ce pas de temps 0.05, on voit également l'écart sur la cinématique transverse :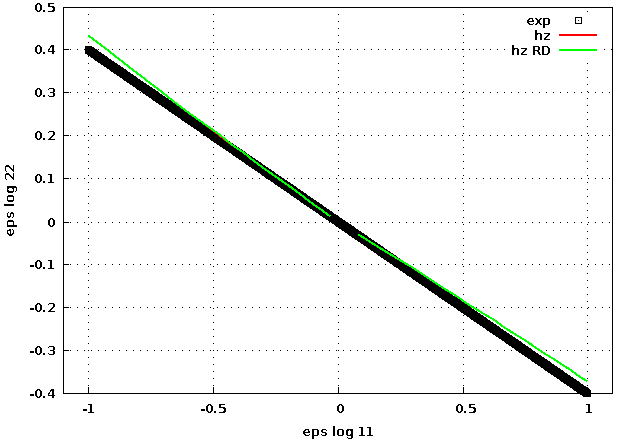
c'est intéressant de voir que l'écart a l'air de même allure en traction et compression. Mais en compression, ça affecte plus la contrainte qu'en traction.
Mis à jour par Gérard Rio il y a environ 2 ans
- Statut changé de En cours à Résolu
- % réalisé changé de 90 à 100