Anomalie #364
ouvertfonction nD : erreur pour utiliser la composante EPS33
Ajouté par Julien Troufflard il y a environ 2 ans. Mis à jour il y a presque 2 ans.
Description
Gérard,
j'ai un test de fonction nD qui utilise les grandeurs EPS11, EPS22, EPS33, EPS12, etc... donc tout le tenseur EPS dans des fonctions nD.
A l'exécution, j'ai le message d'erreur :
Erreur : valeur incorrecte de l'énumération en fonction du nombre de composantes : enu= EPS33 nbcomposantes 3 !
IJind(Enum_ddl a,int nbcomposantes)
On dirait donc plutôt un bug et non juste un problème de grandeur non accessible aux fonctions nD. Pour l'instant, il annonce un problème sur EPS33. Je ne sais pas ce qu'il dira sur EPS13 et EPS23.
A noter que ce genre de mise en données fonctionnent sur des éléments membranes (dans ce cas, je n'utilise que EPS11, EPS22 et EPS12 => pas de message d'erreur).
j'ai mis le cas test en pièce jointe (archive qui crée le répertoire pb_enu_EPS33/).
C'est un cas test sur un cube en traction selon X.
merci
Julien
Fichiers
| pb_enu_EPS33.tar (4,78 ko) pb_enu_EPS33.tar | Julien Troufflard, 16/02/2024 11:26 | ||
| fonctions_nD.info (6,73 ko) fonctions_nD.info | Julien Troufflard, 12/03/2024 10:00 | ||
| SIG11_def_log_hz_vs_th.png (23,3 ko) SIG11_def_log_hz_vs_th.png | Julien Troufflard, 12/03/2024 10:01 | ||
| clipboard-202403132056-4lo0l.png (381 ko) clipboard-202403132056-4lo0l.png | Gérard Rio, 13/03/2024 20:56 | ||
| clipboard-202403132059-rxjc6.png (487 ko) clipboard-202403132059-rxjc6.png | Gérard Rio, 13/03/2024 20:59 | ||
| clipboard-202403132109-qzrny.png (1,43 Mo) clipboard-202403132109-qzrny.png | Gérard Rio, 13/03/2024 21:09 | ||
| clipboard-202403140956-icfbf.png (1,3 Mo) clipboard-202403140956-icfbf.png | Gérard Rio, 14/03/2024 09:56 | ||
| clipboard-202403140957-jxxjj.png (609 ko) clipboard-202403140957-jxxjj.png | Gérard Rio, 14/03/2024 09:57 |
Mis à jour par Gérard Rio il y a presque 2 ans
- Statut changé de Nouveau à En cours
- % réalisé changé de 0 à 70
J'ai corrigé le pb.
Chemin faisant, j'ai modifié l'affichage des infos au niveau des fct nD:
- l'affichage était redondant lorsque l'on utilisait par exemple plusieurs fois la même variable, via des fct composés ce qui est le cas dans ce test, et on affichait tous les termes des tenseurs et non uniquement les composantes utilisées
Du coup, la lecture devenait vite illisible !
- avec la version 7.025, l'affichage des arguments est plus compact et plus exploitable pour comprendre une erreur générée par l'appel d'une fct nD
- dans le test herezh (non fast) affiche une erreur (nan) au niveau du calcul de la fct nD "fct_reso_valPropre_coef_T_MAT_1"
je crois qu'il s'agit du pb du calcul d'une racine d'un nombre "très faiblement" négatif .... mais à creuser
Si c'est le cas il faut sans doute borner les faibles valeurs à 0 dans la définition de la fct nD dans la mise en données
NB: avec la version fast, la vérification de type nan au niveau du calcul de la fct nD est simplifiée et en particulier sur ce test on ne voit pas le pb ... du fait que le nan n'est pas utilisé dans la suite de l'exécution !Julien, peux-tu regarder ?
Mis à jour par Julien Troufflard il y a presque 2 ans
oui, ça fonctionne.
pour plus de clarté dans la suite, je note P la fonction fct_reso_valPropre_coef_P_MAT_1 et T la fonction fct_reso_valPropre_coef_T_MAT_1
donc, effectivement, un test juste sur la nullité de P ne suffit pas pour assurer la réussite du calcul de T. Dans la fonction nD du calcul de T, il fallait éviter que P soit exactement nul (division par 0) mais également s'assurer que sqrt(-3./P) soit défini.
Je dois donc faire en sorte que la fonction de T renvoie simplement 1. si P est nul ou positif.
Là où je ne comprends pas ce qui se passe, c'est que si je modifie la fonction de T avec la conditionnelle suivante, ça fonctionne :
fct_reso_valPropre_coef_T_MAT_1 FONC_SCAL_COMBINEES_ND
fct_base= fct_reso_valPropre_coef_P_MAT_1
fct_base= fct_reso_valPropre_coef_Q_MAT_1
fin_fcts_interne_fonction_combinee_
fct= fct_reso_valPropre_coef_P_MAT_1 > 0. ? \
(1./3.)*acos(3.*fct_reso_valPropre_coef_Q_MAT_1*sqrt(-3./fct_reso_valPropre_coef_P_MAT_1)/(2.*fct_reso_valPropre_coef_P_MAT_1)) : 1.
fin_parametres_fonction_combinee_
Donc ce n'est pas logique. Avec une conditionnelle supérieure stricte à 0., j'évite bien la division par 0 dans le cas où P est nul. Mais bizarrement, je m'assure aussi que le terme (-3./P) est strictement négatif et donc le calcul sqrt(-3/P) devrait coincer systématiquement. Et ça ne fonctionne pas si je mets la condition que je pensais logiquement bonne :
fct= fct_reso_valPropre_coef_P_MAT_1 >= 0. ? 1. : \
(1./3.)*acos(3.*fct_reso_valPropre_coef_Q_MAT_1*sqrt(-3./fct_reso_valPropre_coef_P_MAT_1)/(2.*fct_reso_valPropre_coef_P_MAT_1))
J'ai peut-être complètement raté quelque chose dans la compréhension et je souhaiterais pouvoir afficher les valeurs intermédiaires de mes fonctions nD. En particulier P.
C'est quoi la procédure pour afficher les valeurs des fonctions nD. J'ai déjà réussi une fois mais pas moyen de retrouver mon exemple.
Je profite également de l'occasion pour signaler que le symbole "<" ne peut pas être utilisé dans une fonction nD FONC_SCAL_COMBINEES_ND
Ce genre de pb avait déjà été pointé (et résolu) dans le cas d'une courbe 1D COURBE_EXPRESSION_LITTERALE_1D https://herezh.irdl.fr/issues/291
Si je comprends bien, il faudrait gérer au cas par cas ce problème dans chaque fonction nD ou courbe 1D dans le code d'Herezh ?
A noter qu'on évite facilement ce problème en reversant la condition (écrire la condition avec le symbole supérieur ">" au lieu de "<").
donc ce n'est pas bloquant.
Mis à jour par Julien Troufflard il y a presque 2 ans
- Fichier fonctions_nD.info fonctions_nD.info ajouté
- Fichier SIG11_def_log_hz_vs_th.png SIG11_def_log_hz_vs_th.png ajouté
Bon j'ai retrouvé comment afficher le résultat d'une fonction nD. J'avais oublié qu'on ne pouvait pas afficher le résultat d'une fonction intermédiaire. Herezh n'affiche que les entrées et la sortie de la fonction réellement appelée dans le .info.
Dans mon cas par exemple, je voulais voir le résultat de fct_reso_valPropre_coef_P_MAT_1. Mais j'ai une loi de comportement qui appelle fct_Kc_IIepsLog3D_MAT_1 et fct_mu_IIepsLog3D_MAT_1.
De plus, dans une fonction FONC_SCAL_COMBINEES_ND, les fonctions intermédiaires ne sont pas considérées comme des entrées. Donc je ne peux pas non plus accéder à fct_reso_valPropre_coef_P_MAT_1, ni en entrée, ni en sortie.
Donc l'astuce que j'ai c'est d'utiliser une des fonctions fct_Kc_IIepsLog3D_MAT_1 ou fct_mu_IIepsLog3D_MAT_1 pour afficher en résultat les valeurs que je veux regarder. En utilisant fct_mu_IIepsLog3D_MAT_1, j'ai affiché :
- fct_reso_valPropre_coef_P_MAT_1 => rien d'anormal (il est toujours négatif, ce qui est une condition obligatoire pour ne pas avoir un sqrt() d'un nombre négatif). A la rigueur, elle pourrait être nulle, c'est un cas à prévoir, mais je ne l'ai jamais constaté en affichage.
- fct_reso_valPropre_coef_T_MAT_1 => c'est là qu'est le problème. Même en mettant une condition pour s'assurer que fct_reso_valPropre_coef_P_MAT_1 est strictement inférieur à 0, j'ai parfois un "nan" et parfois un résultat, et ceci avec exactement les mêmes entrées (à savoir les composantes EPS11, EPS22, etc...)
ci-dessous un exemple dans lequel j'utilise la fonction fct_mu_IIepsLog3D_MAT_1 pour afficher la valeur de fct_reso_valPropre_coef_T_MAT_1 :
fonction: fct_mu_IIepsLog3D_MAT_1 :
parametres d'appel: para(1)= 0.00171386 para(2)= 0 para(3)= 0 para(4)= 0.00171386 para(5)= 0 para(6)= 0 para(7)= 0 para(8)= 0 para(9)= 0 para(10)= 0.00171386 para(11)= 0 para(12)= 0 para(13)= 0.00171386 para(14)= 0 para(15)= 0 para(16)= 0 para(17)= 0 para(18)= 0 para(19)= 0.00171386 para(20)= 0 para(21)= 0 para(22)= 0 para(23)= 0 para(24)= 0
retour fonction: val(1)= 7.02447e-09
....
fonction: fct_mu_IIepsLog3D_MAT_1 :
parametres d'appel: para(1)= 0.00171386 para(2)= 0 para(3)= 0 para(4)= 0.00171386 para(5)= 0 para(6)= 0 para(7)= 0 para(8)= 0 para(9)= 0 para(10)= 0.00171386 para(11)= 0 para(12)= 0 para(13)= 0.00171386 para(14)= 0 para(15)= 0 para(16)= 0 para(17)= 0 para(18)= 0 para(19)= 0.00171386 para(20)= 0 para(21)= 0 para(22)= 0 para(23)= 0 para(24)= 0
retour fonction: val(1)= nan
....
*** pb sur le calcul de la contrainte: le resultat est soit infini soit un nan mail: 1 ele: 1 npti: 2
j'ai un peu allégé l'affichage pour ne garder que les affichages concernant fct_mu_IIepsLog3D_MAT_1. Au premier pti, on voit les paramètres d'appel et le résultat obtenu, soit 7.02447e-09. Ensuite, ça passe au second pti. Les paramètres d'entrée sont strictement les mêmes, mais en résultat, on a "nan".
Je ne comprends pas cette différence. Néanmoins, ça pointe un problème qui peut arriver (des éventuels "nan" à gérer parmi tous les pti du maillage). Informatiquement, j'aimerais bien comprendre pourquoi tantôt "nan" et tantôt ça passe à entrées égales.
Mais j'ai trouvé comment régler très simplement tout problème.
Dans les fonctions nD en pièce jointe (nouvelle version du fichier fonctions_nD.info), j'ai supprimé la conditionnelle dans fct_reso_valPropre_coef_T_MAT_1. Le coeur de mon problème, c'est de m'assurer que mes fonctions nD me donnent une valeur de module E tangent avec fonction fct_E_IIepsLog3D_MAT_1. Cette fonction prend en paramètre le résultat de fct_IIepsLog_sur_coef_NU_MAT_1. Cette dernière fonction dépend de la norme au carré du tenseur de déformation log (fonction fct_normeCarree_EPSLOG_MAT_1).
Et bien tout simplement, j'ai ajouté un test sur la valeur de fct_normeCarree_EPSLOG_MAT_1 dans la fonction fct_IIepsLog_sur_coef_NU_MAT_1 :
fct_IIepsLog_sur_coef_NU_MAT_1 FONC_SCAL_COMBINEES_ND
fct_base= fct_normeCarree_EPSLOG_MAT_1
fin_fcts_interne_fonction_combinee_
deb_list_var_ C__NU_MAT_1 fin_list_var_
#petit test > 0 qui permet de gerer automatiquement le cas ou norme(EPSLOG) est "nan"
# (on renvoie simplement 0 si fct_normeCarree_EPSLOG_MAT_1 est "nan", nul ou negatif)
fct= fct_normeCarree_EPSLOG_MAT_1 > 0. ? sqrt(fct_normeCarree_EPSLOG_MAT_1/(1. + 2.*C__NU_MAT_1^2)) : 0.
fin_parametres_fonction_combinee_
Ceci va gérer tout "nan" dans n'importe quelle fonction intermédiaire conduisant à une valeur "nan" pour fct_normeCarree_EPSLOG_MAT_1. Et comme version fast les "nan" ne sont pas bloquants, c'est transparent lors du calcul.
En résultat de traction, j'ai bien une résultat Herezh conforme à un polynome théorique donnant la contrainte en fonction de la déformation :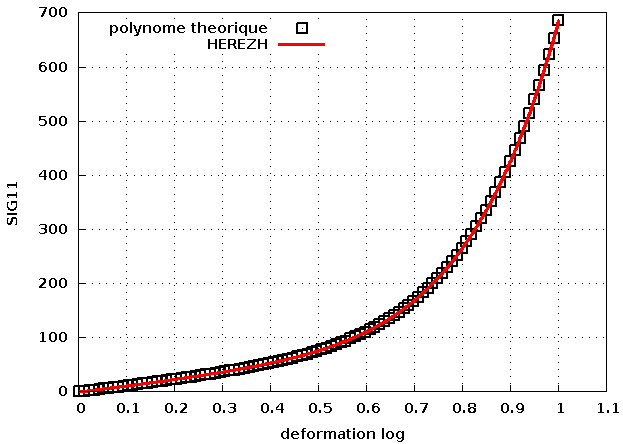
et résultat conforme également en compression uniaxiale.
Mis à jour par Gérard Rio il y a presque 2 ans
cela fait beaucoup de questions ...
Concernant le fait de pb pour des nombres très petits au niveau de la racine carré, je crois me rappeler que j'ai déjà vue ce type de pb et peut-être que la solution est d'être strictement sup à 0 ??? est-ce que c'est un pb de la lib C ou de la lib mu::Parser ?? il faut tester ...
Sinon, au niveau de l'affichage:
- normalement avec un niveau sup à 6 on a tout l'arbre d'appel donc en particulier les fonctions intermédiaires. Par contre cette affichage n'était valable que pour des pb et s’appuyait sur les derniers arguments utilisés.
J'ai étendu l'affichage de tout l'arbre, pour un affichage sans pb pour les arguments courant, en essayant de supprimer les redondances (qui sont redoutables dans ton exemple: on peut avoir plus de 200 redondance d'arguments !! du coup l'affichage est abominable).
Ce n'est pas complètement terminé ...
à suivre
Mis à jour par Gérard Rio il y a presque 2 ans
- % réalisé changé de 70 à 90
bon, après un long et laborieux développement j'arrive à quelque chose d'acceptable pour les fonctions imbriqués.
J'ai essayé d'avoir une sortie synthétique.
Je vais mettre dès que possible la doc à jour.
à suivre
Mis à jour par Gérard Rio il y a presque 2 ans
- Fichier clipboard-202403132056-4lo0l.png clipboard-202403132056-4lo0l.png ajouté
- Fichier clipboard-202403132059-rxjc6.png clipboard-202403132059-rxjc6.png ajouté
- Fichier clipboard-202403132109-qzrny.png clipboard-202403132109-qzrny.png ajouté
- concernant le fait que un < ne fonctionnait pas dans une expression analytique, j'ai modifié, c'est ok
- concernant l'affichage pour une fct nD imbriquée voici qq explication avec comme support la fct: fct_Kc_IIepsLog3D_MAT_1
1) le niveau d'affichage utile ne commence qu'à 4,
. avec un niveau 4, à chaque appel on récupère la valeur de retour de la fonction
ex:
--- fonction: fct_Kc_IIepsLog3D_MAT_1 : ==>> retour fonction: val(1)= 261.453
--- fonction: fct_Kc_IIepsLog3D_MAT_1 : ==>> retour fonction: val(1)= 261.453
...
. avec un niveau 5, on a les variables d'appel (sans les fct internes) et le retour
--- fonction: fct_Kc_IIepsLog3D_MAT_1 :
les_variables_lues: EPS11 = 0.00171386 EPS22 = 0 EPS33 = 0 EPS12 = 0 EPS13 = 0 EPS23 = 0 ==>> retour fonction: val(1)= 261.453
--- fonction: fct_Kc_IIepsLog3D_MAT_1 :
les_variables_lues: EPS11 = 0.00171386 EPS22 = 0 EPS33 = 0 EPS12 = 0 EPS13 = 0 EPS23 = 0 ==>> retour fonction: val(1)= 261.453
...
. avec un niveau 6, on a les variables d'appel, le retour, le nom et la valeur du retour des fonctions internes qui servent d'argument,
--- fonction: fct_Kc_IIepsLog3D_MAT_1 :
les_variables_lues: EPS11 = 0.00171386 EPS22 = 0 EPS33 = 0 EPS12 = 0 EPS13 = 0 EPS23 = 0 ==>> retour fonction: val(1)= 261.453
--- fonction composee : Fonc_scal_combinees_nD : nom_ref= fct_Kc_IIepsLog3D_MAT_1 >>>> fct membres dont le retour sert d'argument: ---
retour fct (fct_E_IIepsLog3D_MAT_1) qui sert d'argument: val(1)= 104.581
retour fct (fct_trace_EPSLOG_MAT_1) qui sert d'argument: val(1)= 0.0017168
...
. avec un niveau 7, idem 6 + les grandeurs globales qui servent d'argument
Supposons que l'on veuille détailler ce qui se passe pour un fonction interne, par exemple ici pour fct_trace_EPSLOG_MAT_1, dans la déclaration de cette fonction on indique un niveau d'affichage qui sera interprété de la même manière que pour la fonction appelante.
Par exemple avec un niveau 7 pour fct_Kc_IIepsLog3D_MAT_1 et 5 pour fct_trace_EPSLOG_MAT_1, on aura:

. avec 6 pour la fonction interne fct_trace_EPSLOG_MAT_1 on a:
on voit que fct_trace_EPSLOG_MAT_1 est elle même une fonction imbriquée qui contient la fct fct_IIepsLog_sur_coef_NU_MAT_1 comme argument
qui est elle même une fonction imbriquée qui contient fct_IIepsLog_sur_coef_NU_MAT_1 qui ..... elle même aussi une fonction imbriquée qui contient 3 fct internes, par exemple fct_IIepsLog_sur_coef_NU_MAT_1 qui aussi est une fct composée etc.
C'est un vrai bin's !!!
supposons que je veux une série de fct avec le niveau 6, cela donne par exemple:

J'ai mis une indentation automatique pour améliorer la lisibilité.
C'est difficile (pour moi) de faire beaucoup mieux vue la complexité des différentes imbrications et la volonté de garder une flexibilité sur l'affichage.
à suivre,
Mis à jour par Julien Troufflard il y a presque 2 ans
merci pour les améliorations et explications
je testerai pour voir.
Je suis un peu obligé de faire des appels d'appels etc... En tout cas, je n'ai pas l'impression que ça plombe le temps de calcul. Un calcul avec une loi de ce genre a l'air de tourner vite et bien sur un cas de Frank.
Mis à jour par Gérard Rio il y a presque 2 ans
- Fichier clipboard-202403140956-icfbf.png clipboard-202403140956-icfbf.png ajouté
- Fichier clipboard-202403140957-jxxjj.png clipboard-202403140957-jxxjj.png ajouté
- % réalisé changé de 90 à 100
la combinaison de fct nD combinées dans le cas ici est effectivement impressionnante, mais... a priori c'est possible.
Du coup, je pense que ce que j'ai mis en place permet d'osculter spécifiquement une fct particulière, en regardant les paramètres d'appel. Par contre il manque une sortie systématique de l'arbre avec uniquement les appels et le retour de chaque fct interne. Ainsi, si on a une interrogation, on peut tout de suite voire où sont les valeurs qui posent pb (pas forcément des nan, mais par exemple des valeurs que l'on n’imaginaient pas ).
Aussi j'ai mis un cas particulier: avec le niveau d'affichage 8 : pour cette valeur indiquée pour une fct nD combinée, il y a affichage de la fct et également des fonctions internes avec le niveau 8 également imposé. Du coup, on obtient directement tout l'arbre d'appel, quelque soit le niveau d'affichage mis en place au niveau des fct internes.
Toujours dans l'exemple de "fct_Kc_IIepsLog3D_MAT_1" voici ce que l'on obtient (je suis obligé de scindé ma copie d'écran en 2, car l'ensemble de l'arbre ne tient pas sur mon écran !!) :
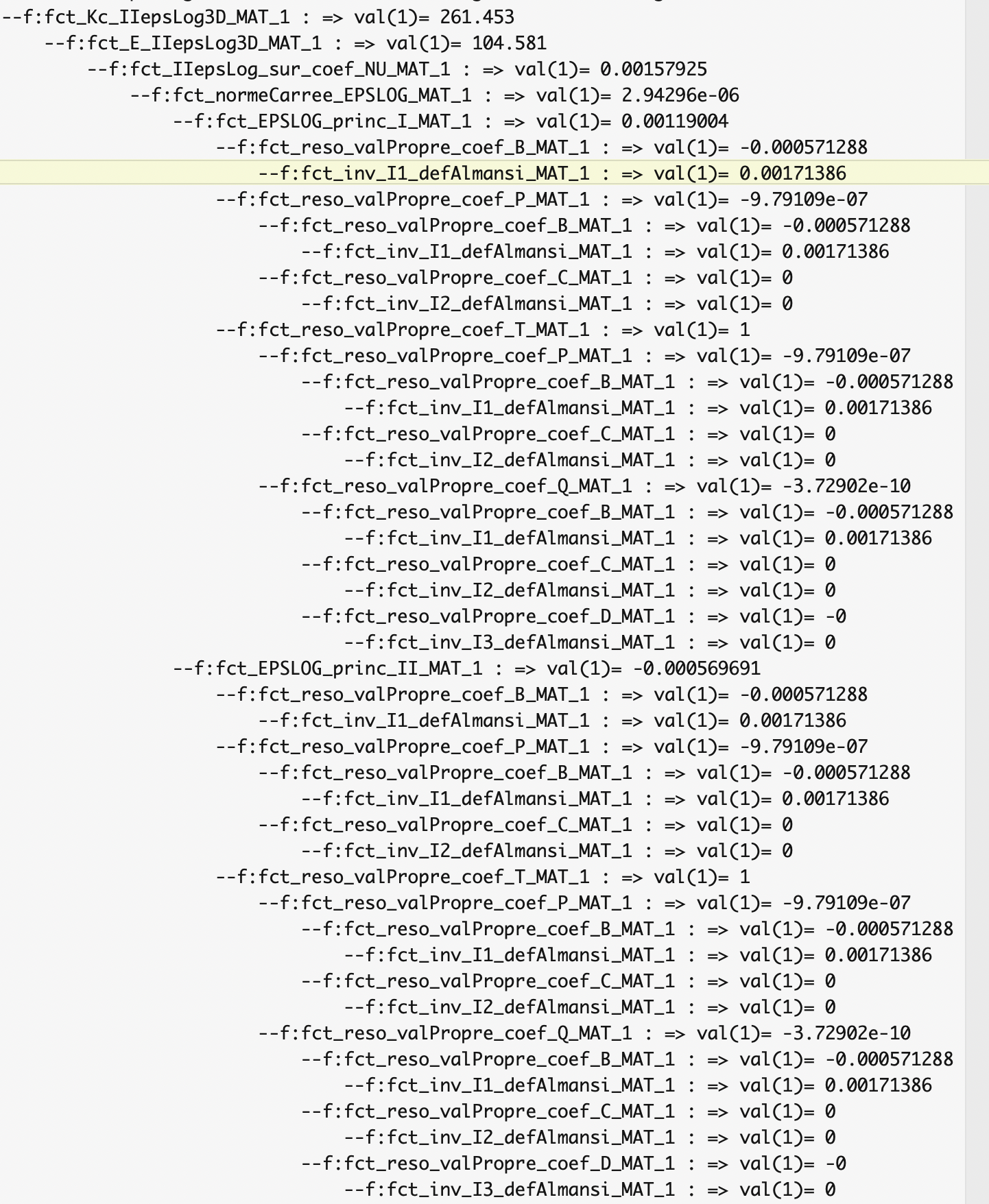

j'arrête là mes développements.