Anomalie #318
ouvertdifficulté convergence MAHEO_HYPER et de son équivalent HYPER_EXTERNE_W (masses nulles en relaxation dynamique)
Ajouté par Julien Troufflard il y a plus de 3 ans. Mis à jour il y a plus de 3 ans.
Description
Gérard,
j'ai un calcul axi de relaxation dynamique qui ne converge pas avec 2 lois de type MAHEO_HYPER.
cf Readme de l'archive jointe.
Il s'agit d'un calcul de bulge axisymétrique en relaxation dynamique.
Le matériau MAT__ est de type MAHEO_HYPER.
Le matériau MAT est de type HYPER_EXTERNE_W et reproduit exactement le comportement de MAHEO_HYPER (car C__w1=1 et C__w2=0 et C__n=1).
Le fichier visu_loi_traction_compression.gnu permet de voir le comportement traction/compression de cette loi => pas de souci particulier sur la courbe contrainte-deformation (idem MAHEO_HYPER). Le coef de Poisson est bruité car il s'agit d'une dérivée numérique (la loi MAHEO_HYPER native donne la même chose en pire).
Quand je lance le calcul calcul_sans_contact_RD.info :
- avec la loi MAT__ (MAHEO_HYPER native) : le calcul bloque dès les premières itérations avec un résidu énorme. Je pense qu'il itère énormément pour la loi contrainte plane. A remarquer que : le coef de compressibilité est très grand. Mais si on le baisse (à 3000 par exemple), ça ne résout pas le problème.
- avec la loi MAT (HYPER_EXTERNE_W) : il calcule des masses nulles.
est-ce qu'il n'y aurait pas un problème de fond sur la relaxation dynamique + loi en invariant de B (et peut-être spécifique à l'axisymétrie).
merci,
Julien
Fichiers
| pb_RD_axi.tar (26,3 ko) pb_RD_axi.tar | Julien Troufflard, 27/07/2022 11:32 | ||
| pb_version_non_AXI.tar (11,4 ko) pb_version_non_AXI.tar | Julien Troufflard, 27/07/2022 12:59 | ||
| calcul_sans_contact_RD_MASS_PHYS.info (2,96 ko) calcul_sans_contact_RD_MASS_PHYS.info | Julien Troufflard, 27/07/2022 20:27 | ||
| nouvelle_version.tar (2,65 ko) nouvelle_version.tar | Julien Troufflard, 28/07/2022 13:38 | ||
| hyper-elasticite.pdf (478 ko) hyper-elasticite.pdf | Nouvelle version transitoires | Gérard Rio, 02/08/2022 11:06 | |
| clipboard-202208021109-uamqd.png (171 ko) clipboard-202208021109-uamqd.png | Gérard Rio, 02/08/2022 11:09 | ||
| test_module_secant.tar (29,2 ko) test_module_secant.tar | Julien Troufflard, 02/08/2022 18:22 | ||
| theorie_herezh++.pdf (5,2 Mo) theorie_herezh++.pdf | Gérard Rio, 03/08/2022 11:37 | ||
| clipboard-202208040911-quosu.png (58,7 ko) clipboard-202208040911-quosu.png | Gérard Rio, 04/08/2022 09:11 | ||
| Kt.png (21,8 ko) Kt.png | Julien Troufflard, 05/08/2022 13:45 | ||
| pression.png (18,9 ko) pression.png | Julien Troufflard, 05/08/2022 13:45 | ||
| theorie_herezh++.pdf (5,2 Mo) theorie_herezh++.pdf | Gérard Rio, 05/08/2022 14:09 | ||
| pression_avec_ecart.png (28,9 ko) pression_avec_ecart.png | Julien Troufflard, 05/08/2022 16:42 | ||
| theorie_herezh++.pdf (5,2 Mo) theorie_herezh++.pdf | Gérard Rio, 08/08/2022 11:29 |
Mis à jour par Julien Troufflard il y a plus de 3 ans
- Fichier pb_version_non_AXI.tar pb_version_non_AXI.tar ajouté
Gérard,
ci-joint une version du calcul axi précédent sans axisymétrie (membrane QUADRANGLE LINEAIRE) avec les mêmes lois. Il y a un peu le même souci. Pas de masses nulles mais un gros problème de loi contrainte plane (qui cherche à établir une épaisseur négative). Donc déjà pas sûr que ça vienne de l'axisymétrie.
J'ai également ajouté une loi mooney-rivlin. Pas l'air de poser problème. Donc a priori pas de problème de fond sur les lois en invariant de B.
A remarquer que la loi MAHEO_HYPER et donc mon potentiel HYPER W est singulier au départ (paramètre de régularisation à 1.e-12). Est-ce que ça viendrait de là ? j'ai essayé plusieurs valeurs de regul à la hausse ou à la baisse => pas d'amélioration
ps : désolé, j'ai mis ce ticket dans Herez++_test sans faire attention.
a+
Julien
Mis à jour par Gérard Rio il y a plus de 3 ans
- Statut changé de Nouveau à En cours
Julien,
avec la loi MAT__ j'obtiens le message suivant:
"
======================================================================
INCREMENT DE CHARGE : 1 intensite 0.01 t= 0.01 dt= 0.01
======================================================================
recalcul de la pseudo-masse (type: 1)
Erreur : (J_r(1)-3.)= -4.44089e-16 est < 0. ! ce n'est pas possible avec les formules actuelles
Maheo_hyper::Calcul_dsigma_deps
passage dans la methode Sortieerreur de loi de comportement element= 96 point d'integration= 3
"Donc là je pense qu'il s'agit d'un pb près de 0.
Avec un facteur de régularisation de e-5 par exemple, c'est ok, mais ensuite vient un pb sur le calcul de l'épaisseur:
" *** pb dans le calcul de la nouvelle epaisseur: le coef de compressibilite moyen = 50880.045 est par rapport a delta la trace de sigma = 838630.29 10 fois inferieur !! ce n'est pas normal a priori on continue sans changer l'epaisseur ...
QuadraMemb::CalEpaisseurMoyenne_et_vol_pti(...)
"
bon... je suis pris cet après-midi,
je regarde demain matin
Mis à jour par Julien Troufflard il y a plus de 3 ans
ok merci.
Au fait, je me disais pourquoi pas essayer avec une matrice masse physique classique. ça serait moins performant, mais juste pour voir si ça tourne. Mais :
1) pas moyen de trouver comment utilise les masses physiques en mode dynamique_relaxation_dynam
2) j'ai essayé en dynamique explicite avec une loi élastique => ça tourne mais pas d'amortissement cinétique
3) idem 2) mais avec loi HYPER_EXTERNE_W => message d'erreur :- erreur, pour l'instant le module d'Young n'est pas calcule !!
Hyper_externe_W::Module_young_equivalent(...
4) et avec MAHEO_HYPER (MAT__), le calcul tourne mais la structure bouge pas beaucoup (pas de temps très petit à cause coef K).
ci-joint un .info en dynamique explicite si besoin
décidement...
Ma priorité reste un calcul dynamique_relaxation_dynam et si possible l'option qui va bien pour avoir les masses physiques.
a+
Julien
Mis à jour par Julien Troufflard il y a plus de 3 ans
- Fichier nouvelle_version.tar nouvelle_version.tar ajouté
Gérard,
bon que des bonnes nouvelles :
1) les lois HYPER_EXTERNE_W ont l'air de tourner en relaxation dynamique si je supprime la partie volumique du potentiel (en mettant C__K3 = 0 dans le fichier de constantes utilisateur) et que l'additionne à une loi ISOHYPERBULK
conclusion : c'est bien la partie volumique de HYPER_EXTERNE_W qui pose problème
2) les calculs de dérivées sont bons dans la partie volumique dans mooney-rivlin du fichier source MooneyRivlin3D.cc ligne 1213
=> r.a.s de ce côté concernant les sources herezh et donc pour toutes les lois genre poly, hart-smith, etc...
(et j'avais une erreur de constante dans le tout 1er fichier potentiel de ce ticket => à écraser par la nouvelle version ci-jointe)
je joins ici des nouveaux fichiers pour pouvoir tester.
J'ai clarifié les noms de loi et de potentiel. Il n'y a plus besoin de changer de potentiel pour changer de loi. Cela se fait directement en changeant de nom de loi (cf la rubrique materiaux du .info ci-joint pour switcher de l'un à l'autre) sachant que :
1) j'ai mis "Natif" quand c'est une loi native Herezh, sinon c'est "HW" quand c'est une version HYPER_EXTERNE_W
2) quand le mot ISOHYPERBULK apparait, ça veut dire que c'est une loi de mélange avec un ISOHYPERBULK natif herezh
==> ATTENTION A BIEN METTRE C__K3 = 0 dans le fichier de constantes utilisateur dans le cas d'une loi additive ISOHYPERBULK + HYPER_EXTERNE_W (et inversement remettre C__K3 = 30000 si la loi n'est pas additive)
ps : c'est un peu bizarre car du coup, la relaxation dynamique fonctionne avec la loi Maheo hyper en version HYPER_EXTERNE_W additionné à ISOHYPERBULK (nom de loi = MAT_HW_Maheo_modifie_ISOHYPERBULK) alors que la loi native MAT_Natif_Maheo_ISOHYPERBULK rencontre toujours un problème comme vu précédemment.
tant mieux pour moi mais donc il y a quelque chose à vérifier dans MAHEO_HYPER. Je vais regarder de mon côté les dérivées dans le code source. Mais j'ai vérifié toutes les lois en traction/compression : à paramètres identiques les lois de même type native, HW additif ou non sont strictement identiques sur une courbe contrainte-déformation. Donc j'y crois pas trop à une erreur de formules de dérivées. à suivre..
bon, déjà, ça fonctionne avec le potentiel HYPER_W, du coup ça devient moins pressant comme demande...
a+
Julien
Mis à jour par Julien Troufflard il y a plus de 3 ans
retour sur dérivées MAHEO_HYPER en natif dans fichier Maheo_Hyper.cc aux alentours de la ligne 712 :
pas d'erreur détectée.
Je me pose juste la question du role de la tournure "exp(-1.5*log(....))" pour la dérivée seconde en ligne 712. Pourquoi ne pas mettre directement : (....)**-1.5 ??
pour la regularisation, je n'ai pas fait la même chose dans HYPER_EXTERNE_W. Si tu veux tester avec mon choix, il suffit d'enlever "fact_regularisation" partout dans les calculs de dérivée et de le mettre à la ligne 701 :
double J_r1moins3 = DabsMaX(J_r(1)-3.+fact_regularisation,0.);
et même manip en ligne 667 + ligne 675
mais aucune idée de si cette intervention aura un impact sur le calcul d'épaisseur.
Mis à jour par Gérard Rio il y a plus de 3 ans
- Fichier hyper-elasticite.pdf hyper-elasticite.pdf ajouté
- Fichier clipboard-202208021109-uamqd.png clipboard-202208021109-uamqd.png ajouté
- % réalisé changé de 0 à 50
Julien,
j'ai retravaillé les développements théoriques et j'ai trouvé des bugs (je ne me rappelle plus où) .
Je te joins les nouvelles formules. Il faut regarder les relations:
- 173 (n'ont pas changé)
- 190, 191, 192 et 193 (les deux premières et la dernière sont nouvelles )
J'ai aussi modifié le code en conséquence et j'ai remplacé les limites (Maxi) par des développements limités, car à la suite d'un petit test sur octave j'ai constaté que les maxi ne marchait pas bien pour V proche de 1. je joins la partie modifiée dans le texte:

Je suis intéressé que tu regardes ... si tu as un moment
Mis à jour par Julien Troufflard il y a plus de 3 ans
- Fichier test_module_secant.tar test_module_secant.tar ajouté
Gérard,
j'ai regardé formules et code. Tout m'a l'air bon dans les dérivées.
Pour le module sécant, les formules 192 sont en accord avec 189 et le code aussi. Mais je ne suis pas sûr d'avoir vraiment compris cette notion de module sécant. Si je comprends bien, le module sécant est la relation entre une variation de pression et une variation de V (V=v/v0). Si non, alors le reste ci-dessous est à mettre à la poubelle :)
mais admettons, si ce module Ks est la relation entre delta(pression) et delta(V), alors ça revient en fait à dire que :
Ks = -d(p)/d(V)
Et du coup, j'ai du mal à comprendre pourquoi il faut postuler une forme pour Ks ( -p = Ks log(V) ) afin d'établir la formule 189.
par exemple, pour les potentiel w (volume actuel) :
si on prend directement la formule 18, ça donne pour un potentiel w :
Ks = -d(p)/d(V) = V.d^2(w)/d(V)^2 + 2*d(w)/d(w)
si on fait un calcul test sur un cube, cette formule pour Ks dédiée au potentiel w est exacte si :
1) on applique un chargement quelconque (traction, oedmétrique, un noeud sur lequel on applique UX,UY,UZ quelconque, etc...)
donc c'est a priori assez général.
2) on prend un loi qui fait la séparation exacte entre variation de volume et variation de forme (donc autre chose que Favier)
donc en gros, cette formule 18 n'est pas juste dédiée aux sollicitations purement sphériques. Du moment que l'on a une loi qui fait bien la séparation, ça marche tout le temps et le module sécant Ks que l'on peut en déduire correspond très bien au résultat donné par Herezh si on calcule la dérivée numérique : Ks = delta Spherique_sig / delta (VOLUME_PTI/volume initial du pti)
si on prend une loi type Favier, ça n'est plus exact car la partie déviatorique devrait entrer en jeu puisqu'elle génère de la variation de volume.
je ne sais pas si c'est utile comme remarque, si ça peut améliorer la convergence, ou si c'est pouillème par rapport à ce qui est déjà implanté.
Concernant les potentiels en invariants J3, je suis donc parti sur l'équation de base (19) => -p = d(W)/d(V)
et j'ai regardé les 4 types de potentiels.
si on suppose Ks = -d(p)/d(V), alors => Ks = d^2(W)/d(V)^2
j'ai regardé le type 2 W = K/2 (V-1) => alors je ne sais pas si cela avait été remarqué avant mais il n'est pas du tout utilisable et je ne l'ai d'ailleurs jamais utilisé. Comme sa dérivée première donne K/2, donc une constante, on obtient une pression hydro constante égale à K/2, même au repos ====> à enlever d'Herezh, non ?
j'ai essayé le type 3 (W = K/2 log(V)**2) => je trouve Ks = d^2(W)/d(V)^2 = K*(1.-log(V))/V**2. Et cette formule correspond bien à la dérivée numérique calculée à partir du .maple de Herezh. Et ça marche pour n'importe quel type de sollicitation (excepté pour Favier). Par contre, le module sécant estimée par l'équation 192 (Ks_3 = K/V) donne un résultat différent.
j'ai essayé le type 1 (W = K*[1- (1 + log(V))/V]) => même remarque que pour type 3. J'ai Ks = K*(1.-2.*log(V))/V**3
et idem pour le type 4 (W = K/2 (V-1)**2 ) => j'ai Ks = K
Et donc pour finir, si je ne me trompe pas :
- dans le cas où la loi fait la séparation exacte volume/forme, l'équation (14) peut devenir générale et non plus dédiée aux seules sollicitations purement sphériques. En fait, cette équation (14) pourrait s'écrire autrement dans le cas général en ne tenant compte que de la partie sphérique de D. On peut alors dans ce cas se contenter d'utiliser les dérivées du potentiel w ou W en suivant l'équation 18 ou 19 pour obtenir le module sécant "exact" avec Ks = d(p)/d(V). pour les lois type Favier/Orgéas, c'est une autre affaire.
j'ai mis en pièce jointe un répertoire pour tester. Voir Readme.
a+
Julien
Mis à jour par Gérard Rio il y a plus de 3 ans
- Fichier theorie_herezh++.pdf theorie_herezh++.pdf ajouté
Julien,
merci pour ta relecture, du coup cela valide ce que je pensais.
Concernant le module de compressibilité, c'est un sujet qui m'a donné du fil à retordre et je n'ai pas vraiment finit de conclure. Je vais essayer de faire une synthèse de ce que j'ai bidouillé.
Tout d'abord l'utilisation du module:
1) il est utilisé pour calculer la variation d'épaisseur pour les éléments plaques et coques et en contrainte plane et la variation de la section pour les éléments barres et en contrainte doublement plane.
2) il "devrait" être utilisé pour le calcul du pas de temps critique, mais dans la pratique c'est un pseudo module d'Young qui est implanté... mais je devrais changer en m'inspirant de ce qui est implanté dans Ls-dyna. Là j'ai déjà avancé mais je n'ai pas concrétisé (à faire dans le futur).
Donc pour l'instant seul 1) est opérationnel. Au niveau théorique pour les contraintes planes, cela correspond (doc: theorie_herezh++.pdf) aux 2 premières formules du chap. 16.1 (formules: 479,480), suivant que l'on considère un module sécant ou un module tangent. Ce qui donne les formules 482 ou 487 (suivant le type de module considéré).
Si le module tangent est constant, en intégrant 480 on obtient une formule de variation globale en log: 485. Mais si le module tangent n'est pas constant, la formule 485 définit un 3 module, le module sécant en log !!
Si le module sécant est constant, on a la formule classique : 479, qui est donc différente de 485.
Donc déjà on voit qu'il faut faire attention à la définition de base de ce que l'on veut appeler "compressibilité". En regardant la littérature dans le domaine, je me suis aperçu qu'il y avait effectivement plusieurs définitions.
Au niveau implémentation, ce n'est pas tout à fait cohérent ce que j'ai fait. Là aussi il faudrait que j'améliore.
a) au niveau du calcul de la variation d'épaisseur en CP, j'ai utilisé directement la formule de variation globale en log: 485 . Donc ce sera d'autant plus juste que le module sera constant et faux s'il varie beaucoup... Il faut noter que la variation d'épaisseur est celle relative à la loi, c'est une variation d'épaisseur que je qualifie de "mécanique".
b) par contre, la loi est utilisée avec des éléments plaques ou coques et là, je calcule une variation d'épaisseur que je qualifie de "géométrique", via la formule incrémentale 487 qui donc utilise normalement le module tangent. Il faut noter que j'utilise en fait une moyenne de module tangent pour tous les pti de l'élément pour les quadrangles et les triangles, et pour les SFE, le calcul est effectué pour chaque pti.
C'est la même idée concernant les contraintes doubles, mais là j'utilise directement eps33 et eps22 pour les déformations dites "mécaniques" et la formule incrémentale 493 pour la variation de section.
Donc en résumé, on a l'impression que c'est le module tangent qu'il faudrait toujours calculer.
Et bien c'est le module sécant que je calcule dans les lois !! (en général) mais pas toujours.
Par exemple dans les lois hypo, c'est évidemment le module tangent qui est naturellement calculé.
En fait ce que j'ai prévu, et commencé à implanter, c'est de calculer les deux: tangent et sécant...
à suivre ... (c'est pas fini !)
Mis à jour par Julien Troufflard il y a plus de 3 ans
mouais, on dirait que j'ai confondu module tangent et module sécant. En fait, tout mon pavé parle du module tangent (qui est bon du coup par comparaison entre doc et résultat Herezh). J'ai vérifié que le module sécant des formules 192 donnent bien -p = Ks*log(V) à tout instant d'un calcul et ça fonctionne pour les potentiels type 1, 3 et 4. Je n'ai pas testé pour les potentiels Favier/Orgéas en petit w.
merci pour les détails. Même si maintenant je suis au clair sur la définition de Ks, je n'en comprends toujours pas l'utilité. Si je veux faire un peu l'analogie avec des lois de comportements utilisateur, en général, on se contente du comportement sécant si on n'a pas réussi à calculer l'opérateur tangent. Donc à vue de nez, si l'opérateur tangent est dispo, il faut l'utiliser sans hésiter.
pour ce qui est de la définition de la compressibilité, pour moi, c'est ce qui relie une variation de pression à une variation de volume, ce qui revient à ce que j'ai écrit précédemment (et c'est bien le K tangent Kt dont il s'agissait) : Kt = -d(p)/d(V). Mais je ne sais pas si c'est la bonne définition (que dit la thermodynamique ?)
Mis à jour par Julien Troufflard il y a plus de 3 ans
pour info, si on commence juste par regarder "saint" wikipedia, il est écrit concernant l'aspect thermodynamique que la compressibilité (isotherme) x_T est :
x_T = 1/K = - 1/v d(v)/d(p)
donc => K = - v d(p)/d(v)
et là, ça parle bien de v comme étant le volume actuel et non la variation de volume V = v/v0
si j'en reviens à Kt = -d(p)/d(V) avec V=v/v0, alors ça collerait à peu près :
=> Kt = -d(p)/d(v/v0) = - v0 d(p)/d(v)
la différence est que dans cette dernière formule, c'est v0 qui est en facteur et non v le volume actuel. Dis autrement, à quel volume faut-il se rapporter pour bien définir la notion de "module de compressibilité" ?
je n'ai pas le temps de creuser des vraies pistes biblio et il me semble que la question, c'est définir un module tangent qui va servir à établir un état d'équilibre mécanique dans un processus itératif (contrainte plane, etc...). Donc s'il y a un peu d'approximation sur le Kt, du moment que ça converge, normalement l'état d'équilibre sera correct. C'est pas ce Kt qui sert à calculer les contraintes.
Mis à jour par Julien Troufflard il y a plus de 3 ans
une dernière remarque qui me vient en rangeant mon répertoire de test :
dans le code pour Ks pour le potentiel type 4, tu es obligé de passer par un développement limité pour éviter des problèmes numériques (suite test sur octave).
Mais en fait, pourquoi ne pas tout simplement mettre que si VmoinsUn < "petit", alors Ks = K ? parce que si V tend vers 1, alors (V-1)/ln(V) tend vers 1.
pas d'avis pour gérer le type 2.
Mis à jour par Gérard Rio il y a plus de 3 ans
- Fichier clipboard-202208040911-quosu.png clipboard-202208040911-quosu.png ajouté
Julien,
juste concernant ta remarque concernant le développement limité: oui on pourrait mettre la limite, mais je pense que c'est plus satisfaisant d'avoir une meilleur continuité à l'interface du "petit" ...
Ceci étant, si ConstMath::petit est suffisamment petit le résultat doit être quasiment identique.
Pour info voici les constantes qui sont implantées et qui sont utilisées dans tout Herezh++: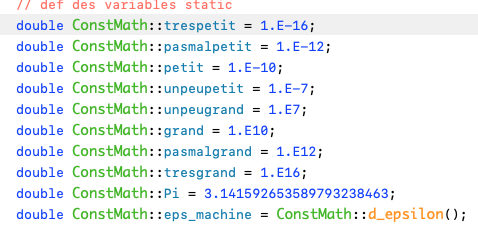
Concernant la définition de Kt que j'ai introduite en 480, c'est bien une division par v et non v0 que j'utilise donc c'est exactement celle que tu as trouvé dans wikipedia.
Pour autant le pb n'est pas tant le choix d'une définition, mais plutôt: à quoi cela va servir. Car en fait dans mes développements théoriques, la compressibilité est une grandeur intermédiaire qui sert à plusieurs choses. L'important, je crois c'est que l'utilisation soit cohérente avec la définition... ce qui n'est pas tout à fait le cas dans Herezh pour l'instant.
Suite du #9 en réponse à #8
Je suis d'accord avec ta remarque ( -p = Ks log(V) ) en fait défini un module sécant "pour une variation en log" donc c'est différent du Ks du 479 et c'est également différent du Kt du 480 "sauf si Kt est constant" (cf. 485).
Je vais clarifier la chose dans la doc théorique et je vais l'appeler : -p = K_slog log(V)
NB: on retrouve finalement le même type de différence que sur la notion de déformation.
Si je reviens sur l'utilisation du module de compressibilité, K_slog est uniquement utilisé en CP, pour calculer la variation d'épaisseur dite mécanique.
Je pourrais me débrouiller pour éviter, et par exemple utiliser eps33 en tenant compte des différents types de def utilisés... (à voir)
Du coup, on pourrait peut-être tout ramener au module tangent.
Si je reviens sur le cas des lois hyper-élastique, les formules de départ sont: 18 ou 19 (suivant que l'on calcule le potentiel sur le volume initial ou final).
Une remarque concernant le chap. 2.1 de hyper-elasticite.pdf:
Je me place dans un cas purement sphérique de vitesse de déformation pour exhiber la partie pression qui concerne la partie purement sphérique du tenseur de contrainte relativement à une partie purement sphérique du tenseur D.
Si on considère un comportement isotrope, a priori il y aura toujours ce type de découpage: D sphérique vs pression, et D déviatorique versus contrainte déviatorique.
Mais on peut étendre les formule.
Donc oui, les formules 18 et 19 sont correctes pour un matériau hyper-élastique isotrope.
Je vais généraliser dans un cas quelconque, je vais mettre à jour la doc... à suivre
Pour les potentiels utilisant les invariants de Mooney-Rivlin on a directement 188, et effectivement, si on s'attache uniquement à calculer le module tangent on peut directement dérivée 2 fois la formule 18, et donc pour les potentiels implantés on peut ne retenir que la partie volumique du potentiel qui est clairement différencié. Du coup on obtiendra directement K_t.
Les formules que j'ai calculées sont donc relatives à K_slog.
Je vais compléter avec les formules en K_t
Pour les potentiels en V, Qeps et phase que j'appelle de "Grenoble" car Favier et Orgéas sont de Grenoble (c'est historique), je vais préciser la chose, mais on peut également étendre les formules
à suivre ...
Mis à jour par Julien Troufflard il y a plus de 3 ans
pas évident à bien cerner toutes les formules doc théorique.
j'ai vite fait regardé. vu pour la formule (480), effectivement ça colle avec Kt = - v d(p)/d(v)
j'ai un peu plus de mal sur la formule (485). Elle découle sans problème de (484) si Kt constant mais au final, comment (485) peut être vraie : -p = Kt log(vol). On a bien vol = v en terme de notation. Donc si Kt est en MPa et log(vol) en unité de volume, alors -p ne peut pas être en MPa. Et d'ailleurs, ça supposerait que à l'état inital, on aurait -p_0 = Kt log(vol_0), donc une valeur non nulle si vol_0 n'est pas dans le cas particulier vol_0 = 1.
pour ce qui est de Kt pour les potentiels de Grenoble, j'ai constaté que la dérivée numérique delta(p)/delta(V) ne donnait pas la même chose que la dérivée de l'équation (18) pour une sollicitation quelconque. La partie déviatorique génère de la pression. Et donc je comprends bien que ce chapitre 2.1 soit restreint aux sollicitations purement sphérique. Parce que dans le cas général, on ne peut pas dire qu'un matériau isotrope suffise à avoir un découpage: D sphérique vs pression, et D déviatorique versus contrainte déviatorique. Pour les lois hyperélastique en invariant d'Almansi ou une simple loi ISOELAS qui utilise Almansi, ça ne fonctionnera pas. Pour calculer le Kt, une relation entre p et V ne sera pas suffisante.
Mis à jour par Gérard Rio il y a plus de 3 ans
Il y a une erreur dans ma formule !
c'est : -P = Kt (log(vol) - log(vol_0) ) = K_t log(vol/vol_0)
Comme quoi c'est important de commencer par vérifier la théorie !!
Concernant les potentiels de Grenoble:
- pour une cinématique de vitesse de déformation purement sphérique, les formules 18 et 19 sont toujours valables, quelque soit la loi hyperélastique (Grenoble y compris) car elles ne font pas intervenir le contenu du potentiel, ni le type de mesure de déformation. Donc on peut les utiliser pour le calcul des modules Ks, Kt et Kslog, qui sont tous les 3 relatif à un D sphérique c-a-d une variation pure de volume.
Il faut remarquer que dans ces formules on utilise des dérivées partielles. Donc si on considère les potentiels de Grenoble avec les invariants V, Qeps et phi, lorsque l'on fait une dérivée partielle par rapport à V, on impose que les deux autres invariants sont constants. En fait c'est aussi vrai, quelque soit les deux autres invariants (diff de V) retenue.
Donc je pense que les formules 18, 19 sont utilisables également pour les potentiels de Grenoble...
à suivre,
Mis à jour par Julien Troufflard il y a plus de 3 ans
- Fichier Kt.png Kt.png ajouté
- Fichier pression.png pression.png ajouté
concernant : -P = Kt (log(vol) - log(vol_0) ) = K_t log(vol/vol_0)
=> ok, mais du coup, ça serait pas plutôt Ks ? ça ressemble à la définition de Ks. Un peu la même remarque sur équation (480), il y a tantôt Kt, tantôt Ks.
concernant loi Grenoble :
=> alors là j'ai du mal à comprendre. J'ai repris mon répertoire de test de Kt pièce jointe précédente. J'ai calculé une loi Favier (MAT_2), sa dérivée numérique (script perl) et regardé le résultat avec fichier gnu_petit_w. Je n'ai pas fait d'erreur dans les formules. Et pourtant, pour une sollicitation quelconque, effectivement je suis d'accord avec toi, la formule (18) fonctionne pour calculer la pression (pièce jointe pression.png).
Par contre, j'ai des oscillations en calculant Kt (pièce jointe Kt.png). Le comportement tangent par dérivation du calcul Herezh ne donne pas pareil exactement pareil que la formule théorique : Kt = - d(p)/d(V) avec V=v/v0. Je vois bien que l'échelle du graphe est très zoomé, donc le résultat est grosso modo pas mal. Mais je n'avais pas de telles d'oscillations avec les modèles en invariant de B.
Et malgré tout, ce graphe a l'air d'aller dans ton sens (formule (18) vraie aussi pour Almansi dans le cas général, et donc ses dérivées => Kt). Au final, comme Favier/Orgéas est lié à un tenseur de trace nulle, il ne génère pas de pression hydro. Et pourtant, je sais qu'Almansi ne fait pas la décomposition volume-forme. ça me laisse un peu perplexe. Je ne suis pas encore bien persuadé. L'oscillation de la courbe Kt.png me donne l'impression qu'il y a un problème, même si léger.
Mis à jour par Julien Troufflard il y a plus de 3 ans
ps : bon en fait on s'en fout de Kt ou Ks dans (485). Si Kt constant => Kt = Ks.
ps 2 : Peut-être préciser que (486) découle de (480).
Mis à jour par Gérard Rio il y a plus de 3 ans
- Fichier theorie_herezh++.pdf theorie_herezh++.pdf ajouté
oui,
-P = Kt (log(vol) - log(vol_0) ) = K_t log(vol/vol_0)
correspond à Kt si Kt constant,
mais de manière générale c'est effectivement un Ks, que j'ai appelé K_s,log, car il s'agit d'un K sécant pour une variation log.
J'ai mis à jour la doc théorique, voir le chap 16.1
Pour les lois de Grenoble, c'est effectivement assez dur à comprendre, c'est un peu pour cela que je voulais échanger de vive voix,
à suivre,
bonne réunion
Mis à jour par Julien Troufflard il y a plus de 3 ans
- Fichier pression_avec_ecart.png pression_avec_ecart.png ajouté
je suis dispo si besoin pour appel.
et sinon, pour revenir sur mes graphes précédents :
j'ai modifié mon graphe "pression.png" pour mieux comprendre. ci-joint même graphe mais avec ajout de l'écart relatif en % entre simulation et théorie équation (18). Et donc, là, je comprend mieux. Il n'y a pas égalité entre pression simulée et pression théorique(18). Il y a un écart même si faible. Le fait d'utiliser la déf d'Almansi conduit bien à une influence sur le volume même si on utilise que sa partie déviatorique.
Et on le voit bien sur un essai de cisaillement simple. Si tu prends un cube 1x1x1, que tu lui mets les conditions X Y pour faire du cisaillement dans le plan XY, et que tu bloques une des faces selon Z, ça donne bien :
- si loi en invariant almansi => variation de l'épaisseur du cube le long de Z => volume diminue
- si loi en invariant de B => pas de variation (volume reste à 1)
Et j'ai donc fait l'erreur d'associer volume et trace nulle du tenseur de déf. La partie déviatorique Almansi ne génère pas directement de termes sur la trace de sigma mais elle influencera le volume donc la pression.
ça veut dire la formule (18), dans le cas général pour Almansi, devrait introduire des termes liés à la dérivation par rapport à Q_eps.
Parce que la comparaison à la simulation montre que :
1) pour une valeur de V donnée, il y a un écart entre théorique(18) et simulation. Donc il y a quelque chose qui manque dans la dérivée première du potentiel selon V.
2) pas exact non plus Kt. Donc => manque aussi quelque chose dans les dérivées secondes
Mis à jour par Gérard Rio il y a plus de 3 ans
oui je suis d'accord avec ton analyse.
Les formules 18 et 19 sont exactes ... dans le cadre d'une cinématique en vitesse de déformation sphérique, et que dans ce cadre.
Si on est dans un cadre quelconque, dans la dérivée du potentiel (terme de droite de 17) il faut considérer les 3 invariants. Du coup, va apparaitre, dans le cas des potentiels de Grenoble, les termes de couplage avec V et donc on obtiendra une formule qui intègre des termes supplémentaires à 18 , provenant des couplages de Qeps et de cos3phi avec V.
Donc c'est cohérent avec les tests que tu as menés.
Ma conclusions est la suivante:
- pour des potentiels qui n'ont pas de couplage, 18 et 19 sont opérationnelles.
- pour des potentiels avec couplage, 18 et 19 sont une approximation qui est d'autant meilleur que le couplage est faible (disons pour une def < 10%) ce qui est cohérent avec les tests qu'avaient effectués Denis Favier. Donc pour des AMF, c'est ok, pour des polymères cela peut limiter leur domaine d'utilisation.
D'autre part le couplage (a priori) introduit ds les potentiels Grenoblois une non unicité de la solution à partir d'une certaine def (environ > 10%). Donc c'est problématique au niveau numérique avec un schéma de type Newton.
Une amélioration est d'utiliser la def de Hencky. J'ai fait les développements numériques dans le document, il faut que j'implante ! à faire ...
Mais pour l'instant je retiens qu'il faut que j'implante le calcul systématique de Kt pour toutes les lois. Tans que j'y suis je vais voir pour implanter également les deux autres modules si cela ne pose pas de pb, d'où dans une première étape, je vais regarder d'un point de vue théorique ce que cela implique: Kt d'abord puis Ks et Kslog.
àsuivre
Mis à jour par Gérard Rio il y a plus de 3 ans
- Fichier theorie_herezh++.pdf theorie_herezh++.pdf ajouté
- % réalisé changé de 50 à 60
modif théorie,
- précisions apportées aux modules de compressibilités : K_s devient K_{s1} et K_{s2} avec une remarque lorsque K_{s2} est constant (chap. 16.1)
- pour l'élasticité de Hooke: calcul de l'approximation du module tangent dans le cas de faible déformation d'Almansi et dans le cas de def log